Cho \(a,b,c>0\), tìm giá trị nhỏ nhất của biểu thức:
A\(=\dfrac{a}{\sqrt{ab+b^2}}+\dfrac{b}{\sqrt{bc+c^2}}+\dfrac{c}{\sqrt{ca+a^2}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(12\dfrac{1}{3}-10\dfrac{1}{4}\right):\left(2\dfrac{1}{2}+1\dfrac{1}{3}\right)\\ =\left(\dfrac{37}{3}-\dfrac{41}{4}\right):\left(\dfrac{5}{2}+\dfrac{4}{3}\right)\\ =\dfrac{25}{12}:\dfrac{23}{6}\\ =\dfrac{25}{12}\cdot\dfrac{6}{23}\\ =\dfrac{25}{46}\)

Số m vải còn lại sau khi bán ngày 1 chiếm:
1 - 3/5 = 2/5
Số m vải còn lại sau khi bán ngày 2 chiếm:
2/5 - 2/5 . 2/7 = 2/7
Số mét vải cửa hàng đã bán:
40 : 2/7 = 140 (m)

\(x^2-2x+m=0\Leftrightarrow x^2-2x-3=-m-3\)
Từ đồ thị ta thấy:
a.
Phương trình vô nghiệm khi \(-m-3< -4\Rightarrow m>1\)
b.
Phương trình có nghiệm kép khi \(-m-3=-4\Rightarrow m=1\)
c.
Phương trình có 2 nghiệm pb khi:
\(-m-3>-4\Rightarrow m< 1\)
d.
Phương trình có 2 nghiệm pb thuộc \(\left[-1;3\right]\) khi: \(-4< m\le0\)
e.
Có 2 nghiệm pb ko thuộc \(\left[-1;3\right]\) khi \(m>0\)

Xét ΔAHB vuông tại H có \(tanBAH=\dfrac{BH}{AH}\)
=>\(BH=AH\cdot tanBAH=4\cdot tan28\simeq2,13\left(cm\right)\)
Xét ΔAHC vuông tại H có
\(tanC=\dfrac{AH}{HC}\)
=>\(HC=\dfrac{AH}{tanC}=\dfrac{4}{tan40}\simeq4,77\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AB=\sqrt{AH^2+HB^2}\simeq4,53\left(cm\right)\)
ΔAHC vuông tại H
=>\(AH^2+HC^2+AC^2\)
=>\(AC=\sqrt{AH^2+HC^2}\simeq6,23\left(cm\right)\)


Trung bình mỗi tổ làm được:
\(\left(\dfrac{1}{3}+\dfrac{2}{3}+\dfrac{1}{6}\right):3=\dfrac{7}{6}:3=\dfrac{7}{18}\)(công việc)
Trung bình mỗi tổ làm được số phần công việc là:
`(1/3 + 2/3 + 1/6) : 3 = 7/18` (công việc)
Đáp số: `7/18` công việc
----------------------------------
- Nếu xét tính đúng sai của đề toán thì đề này hoàn toàn sai so với thực tế rồi bạn nhé. Số công việc được quy về làm 1 đơn vị
Mà `1/3 + 2/3 + 1/6 = 7/6 > 1` có nghĩa là cả 3 tổ không làm nhiều đến mức như trong đề ra

Tổng số bao ngô tổ 1 chở là 3x36=108(bao)
Tổng số bao ngô tổ 2 chở là 6x27=162(bao)
Tổng số bao ngô hai xe là 108+162=270(bao)
Tổng khối lượng ngô là 270x4=1080(yến)=10800(kg)
Trung bình mỗi xe chở:
10800:(3+6)=10800:9=1200(kg)
Tổng số bao ngô tổ 1 chở là
3x36=108(bao)
Tổng số bao ngô tổ 2 chở là
6x27=162(bao)
Tổng số bao ngô hai xe là
108+162=270(bao)
Tổng khối lượng ngô là
270x4=1080(yến)=10800(kg)
Trung bình mỗi xe chở:
10800:(3+6)=10800:9=1200(kg)
đáp số:....
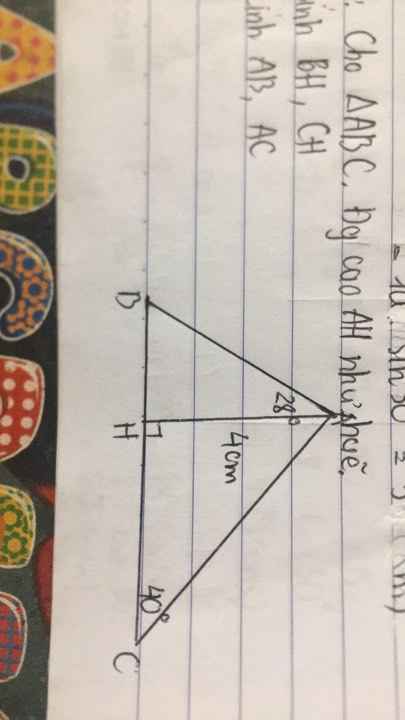
\(A=2\sqrt{2}\left(\dfrac{a}{2\sqrt{2b\left(a+b\right)}}+\dfrac{b}{2\sqrt{2c\left(b+c\right)}}+\dfrac{a}{2\sqrt{2a\left(c+a\right)}}\right)\)
\(A\ge2\sqrt{2}\left(\dfrac{a}{2b+a+b}+\dfrac{b}{2c+b+c}+\dfrac{a}{2a+c+a}\right)\)
\(A\ge2\sqrt{2}\left(\dfrac{a^2}{a^2+3ab}+\dfrac{b^2}{b^2+3bc}+\dfrac{c^2}{c^2+3ca}\right)\)
\(A\ge\dfrac{2\sqrt{2}\left(a+b+c\right)^2}{a^2+b^2+c^2+3\left(ab+bc+ca\right)}=\dfrac{2\sqrt{2}\left(a+b+c\right)^2}{\left(a+b+c\right)^2+ab+bc+ca}\)
\(A\ge\dfrac{2\sqrt{2}\left(a+b+c\right)^2}{\left(a+b+c\right)^2+\dfrac{1}{3}\left(a+b+c\right)^2}=\dfrac{3\sqrt{2}}{2}\)
Dấu "=" xảy ra khi \(a=b=c\)
Bổ sung các bđt được áp dụng trong bài thầy Lâm cho rõ ràng:
Áp dụng Bđt Cauchy và Bunhiacopxki :
\(a+3b=2b+\left(a+b\right)\ge2\sqrt[]{2b\left(a+b\right)}\)
\(ab+bc+ca\le\sqrt[]{\left(a^2+b^2+c^2\right)\left(a^2+b^2+c^2\right)}=a^2+b^2+c^2\)