Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo đề ta có:
7 + 9 + 7 + 8 + x + y = 50
x + y = 50 - 7 - 9 - 7 - 8 = 19
x + x + 1 = 19 (vì x < y và x và y là hai số tự nhiên liên tiếp)
2x = x + x = 19 - 1 = 18
x = 18 : 2 = 9, suy ra y = 9 + 1 = 10
Vậy xác suất thực nghiệm của sự kiện: "Gieo được mặt 6 chấm trong 50 lần giao trên) là 10 : 50 = 0,2

\(2x^2-2xy-4x+y^2+4=0\)
\(\Leftrightarrow x^2-2xy+y^2+x^2-4x+4=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-2\right)^2=0\left(1\right)\)
mà \(\left\{{}\begin{matrix}\left(x-y\right)^2\ge0,\forall x;y\\\left(x-2\right)^2\ge0,\forall x\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)^2=0\\\left(x-2\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)

4\(x^2\) + y2 - 12\(x\) + 10y + 34 = 0
(4\(x^2\) - 12\(x\) + 9) + (y2 + 10y + 25) = 0
(2\(x\) - 3)2 + (y + 5)2 = 0
(2\(x\) - 3)2 ≥ 0 ∀ \(x\); (y + 5)2 ≥ 0 ∀ y
(2\(x-3\))2 + (y + 5)2 = 0 ⇔ \(\left\{{}\begin{matrix}2x-3=0\\y+5=0\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-5\end{matrix}\right.\)
Kl: (\(x;y\)) = ( \(\dfrac{3}{2}\); -5)

\(\dfrac{13}{6}:x=2-\dfrac{2}{5}\)
\(\dfrac{13}{6}:x=\dfrac{10}{5}-\dfrac{2}{5}\)
\(\dfrac{13}{6}:x=\dfrac{8}{5}\)
\(x=\dfrac{13}{6}:\dfrac{8}{5}\)
\(x=\dfrac{13}{6}x\dfrac{5}{8}\)
\(x=\dfrac{65}{48}\)

\(4x^2+y^2-12x+10y+34=0\)
\(\Leftrightarrow4x^2-12x+9+y^2+10y+25=0\)
\(\Leftrightarrow\left(2x-3\right)^2+\left(y+5\right)^2=0\left(1\right)\)
mà \(\left\{{}\begin{matrix}\left(2x-3\right)^2\ge0,\forall x\\\left(y+5\right)^2\ge0,\forall y\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3\right)^2=0\\\left(y+5\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3=0\\y+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-5\end{matrix}\right.\)
Ta có : \(4x^2+y^2-12x+10y+34=0\)
\(\Leftrightarrow4x^2-12x+9+y^2+10y+25=0\)
\(\Leftrightarrow\left(2x-3\right)^2+\left(y+5\right)^2=0\left(1\right)\)
Ta thấy : \(\left(2x-3\right)^2;\left(y+5\right)^2\ge0\)
Nên để (1) thoả mãn :
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3=0\\y+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-5\end{matrix}\right.\)
Vậy........

2\(\dfrac{5}{4}\) là một hỗn số hả em, như vậy không hợp lý vì phần phân số phải bé hơn 1

\(5km460m=5460m\)
Số m đội 1 sửa được :
\(5460.\dfrac{1}{3}=1820\left(m\right)\)
Số m đội 2 sửa được :
\(1820.\dfrac{3}{4}=1365\left(m\right)\)
Số m đội 3 sửa được :
\(5460-\left(1820+1365\right)=2275\left(m\right)\)
Số m mỗi buổi sửa được :
\(5460:3=1820\left(m\right)\)
Đổi 5km 460 m = 5460 m
Đội 1 sửa được: 5460 \(\times\) \(\dfrac{1}{3}\) = 1820 (m)
Đội 2 sửa được: 1820 \(\times\) \(\dfrac{3}{4}\) = 1365 (m)
Đội 3 sửa được: 5460 - 1820 - 1365 = 2275 (m)
Đs..

Chiều rộng là: 25 \(\times\) \(\dfrac{3}{5}\) = 15 (m)
Diện tích mảnh vườn hình chữ nhật là: 25 \(\times\) 15 = 375 (m2)
đs..

Số tấn thóc kho thứ 2 chứa :
\(4008-351=3657\left(tấn\right)\)
Số tấn thóc kho thứ 3 chứa :
\(3657+105=3762\left(tấn\right)\)
Số tấn thóc trung bình mỗi kho chứa :
\(\left(4008+3657+3762\right):3=3809\left(tấn\right)\)
kho thứ hai chứa được số tấn thóc là: 4008 - 351 = 3657(tấn thóc)
kho thứ ba chứa được số tấn thóc là : 3657 + 105 = 3762(tấn thóc)
tổng số tấn thóc của cả ba kho là : 4008 + 3657 + 3762 = 11427(tấn thóc)
trung bình mỗi kho chứa được số tấn thóc là : 11427 : 3 = 3809(tấn thóc)
Đ/S:...................

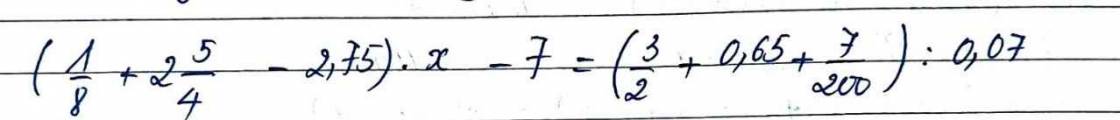
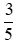
\(\Leftrightarrow4x^2-12x+9+y^2+10y+25=0\)
\(\Leftrightarrow\left(2x-3\right)^2+\left(y+5\right)^2=0\) (1)
Do \(\left(2x-3\right)^2\ge0\) và \(\left(y+5\right)^2\ge0\)
\(\Rightarrow\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3\right)=0\\y+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-5\end{matrix}\right.\)