Một mảnh vườn hình chữ nhật có chu vi 92 m. Nếu tăng chiều rộng thêm 5 m và giảm chiều dài đi cũng 5 m thì mảnh vườn sẽ trở thành hình vuông. Tính diện tích ban đầu của mảnh vườn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi \(P=2+2^2+2^3+...+2^{120}\)
\(\Rightarrow2P=2^2+2^3+2^4+...+2^{121}\)
\(\Rightarrow P=2P-P=2^{121}-2\)
Ta đi chứng minh \(2^{121}-2⋮17\) hay \(2^{120}-1⋮17\)
Thật vậy, dễ dàng kiểm tra \(2^8-1⋮17\). Lại có \(2^{120}-1=\left(2^8\right)^{15}-1\) \(⋮2^8-1⋮17\) nên suy ra \(2^{120}-1⋮17\).
(Áp dụng tính chất \(a^n-1⋮a-1\) với mọi số nguyên \(a\) khác 1 và số tự nhiên \(n\))
Từ đó suy ra đpcm.

Lời giải:
Nếu $x\geq 3$ thì:
$5=|x-3|-|2-x|=(x-3)-(x-2)=-1$ (vô lý - loại)
Nếu $2\leq x<3$ thì:
$5=|x-3|-|2-x|=(3-x)-(x-2)=5-2x$
$\Rightarrow x=0$ (vô lý - loại do $x\geq 2$)
Nếu $x<2$ thì:
$5=|x-3|-|2-x|=(3-x)-(2-x)=1$ (vô lý - loại)
Vậy không tồn tại $x$ thỏa đề.

Lời giải:
\(ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-2}{2}=1\)
Khi đó:
\(\text{VT}=\frac{a}{ab+bc+ac+a^2}+\frac{2b}{ab+bc+ac+b^2}+\frac{3c}{ab+bc+ac+c^2}\)
\(=\frac{a}{(a+b)(a+c)}+\frac{2b}{(b+a)(b+c)}+\frac{3c}{(c+a)(c+b)}\)
\(=\frac{a(b+c)+2b(a+c)+3c(a+b)}{(a+b)(b+c)(c+a)}\)
\(=\frac{3ab+4ac+5bc}{(a+b)(b+c)(c+a)}=\text{VP}\)

`#040911`
`a,`
\(\left|2x-25\right|=41\)
\(\Rightarrow\left[{}\begin{matrix}2x-25=41\\2x-25=-41\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=41+25\\2x=-41+25\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=66\\2x=-16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=66\div2\\x=-16\div2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=33\\x=-8\end{matrix}\right.\)
Vậy, `x \in { -8; 33 }`
`b,`
\(\dfrac{11}{3}-\left|\dfrac{5}{4}-x\right|=\dfrac{21}{4}\)
\(\Rightarrow\left|\dfrac{5}{4}-x\right|=\dfrac{11}{3}-\dfrac{21}{4}\)
\(\Rightarrow\left|\dfrac{5}{4}-x\right|=-\dfrac{19}{12}\left(\text{vô lý}\right)\)
Vậy, `x` không có giá trị nào thỏa mãn.
a) |2x - 25| = 41
2x - 25 = 41 và 2x - 25 = -41
*) 2x - 25 = 41
2x = 41 + 25
2x = 66
x = 66 : 2
x = 33
*) 2x - 25 = - 41
2x = -41 + 25
2x = -16
x = -16 : 2
x = -8
Vậy x = -8; x = 33
b) 11/3 - |5/4 - x| = 21/4
|5/4 - x| = 11/3 - 21/4
|5/4 - x| = -19/12 (vô lí vì |5/4 - x| ≥ 0 với mọi x ∈ R)
Vậy không tìm được x thỏa mãn yêu cầu đề bài

Ta thấy : \(\left|x-2021\right|\ge0\forall x,\left|y-2022\right|\ge0\forall y\\ =>\left|x-2021\right|+\left|y-2022\right|\ge0\)
Mà theo đề : \(\left|x-2021\right|+\left|y-2022\right|\le0\)
=> \(\left\{{}\begin{matrix}x-2021=0\\y-2022=0\end{matrix}\right.=>\left(x;y\right)=\left(2021;2022\right)\)

Lời giải:
a. Nếu $x\geq 3$ thì:
$5=|x-3|-|2-x|=(x-3)-(x-2)=-1$ (vô lý - loại)
Nếu $2\leq x<3$ thì:
$5=|x-3|-|2-x|=(3-x)-(x-2)=5-2x$
$\Rightarrow x=0$ (vô lý - loại do $x\geq 2$)
Nếu $x<2$ thì:
$5=|x-3|-|2-x|=(3-x)-(2-x)=1$ (vô lý - loại)
Vậy không tồn tại $x$ thỏa đề.
b.
Vì $|3x+1|\geq 0; |x-4|\geq 0$ với mọi $x$
Do đó để tổng của chúng bằng $0$ thì:
$|3x+1|=|x-4|=0$
Hay $x=\frac{-1}{3}=4$ (vô lý)
Vậy không tìm được $x$ thỏa mãn.

\(\left(x-1\right)^2+\left(y+3\right)^2=0\left(1\right)\)
Ta thấy \(\left\{{}\begin{matrix}\left(x-1\right)^2\ge0,\forall x\\\left(y+3\right)^2\ge0,\forall y\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+3\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=0\\y+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+3\right)^2=0\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}\left(x+1\right)^2=0^2\\\left(y+3\right)^2=0^2\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x+1=0\\y+3=0\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=-1\\y=-3\end{matrix}\right.\)

Gọi d là ƯCLN(4n + 5; 2n + 2)
⇒ (4n + 5) ⋮ d
(2n + 2) ⋮ d ⇒ 2(2n + 2) ⋮ d ⇒ (4n + 4) ⋮ d
⇒ [(4n + 5) - (4n + 4)] ⋮ d
⇒ (4n + 5 - 4n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 4n + 5 và 2n + 2 là hai số nguyên tố cùng nhau
Gọi ước chung lớn nhất của 4n + 5 và 2n + 2 là: d
Ta có: 4n + 5 ⋮ d
2n + 2 ⋮ d
⇒ 2.(2n+ 2) ⋮ d ⇒ 4n + 4 ⋮ d
⇒ 4n + 5 - (4n + 4) ⋮ d
4n + 5 - 4n - 4 ⋮ d
1 ⋮ d ⇒ d = 1
Ước chung lớn nhất của 4n + 5 và 2n + 2 là 1
Hay 4n + 5 và 2n + 2 là hai số nguyên tố cùng nhau

(\(x\) - 2023)\(x-2024\) = 1
⇒ \(\left[{}\begin{matrix}x\ne2023;x-2024=0\\x-2023=1\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}x=2024\\x=2024\end{matrix}\right.\)
Vậy \(x=2024\)
(x - 2023)ˣ⁻²⁰²⁴ = 1
(x - 2023)ˣ⁻²⁰²⁴ = (x - 2023)⁰ (x ≠ 2023)
x - 2024 = 0
x = 2024 (nhận)
Vậy x = 2024
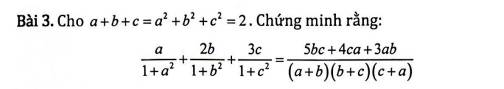
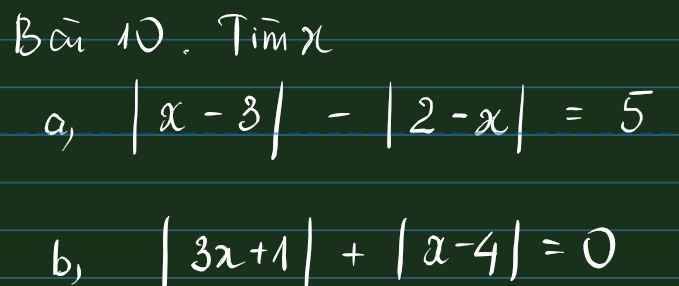
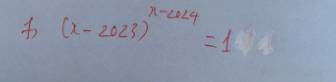
Nửa chu vi mảnh vườn là :
92 : 2 = 46 (m)
Hiệu giữa chiều dài và chiều rộng là :
5 + 5 = 10 (m)
Chiều dài mảnh vườn là :
(46 + 10) : 2 = 28 (m)
Chiều rộng mảnh vườn là :
46 - 28 = 18 (m)
Diên tích mảnh vườn ban đầu là :
28 x 18 = 504 (m2)
Đ/s...
Nửa chu vi vườn HCN :
\(92:2=46\left(m\right)\)
Chiều dài bằng chiều rộng sau khi tăng và giảm là :
\(46:2=23\left(m\right)\)
Chiều rộng vườn HCN ban đầu là :
\(23-5=18\left(m\right)\)
Chiều dài vườn HCN ban đầu là :
\(23+5=28\left(m\right)\)
Diện tích ban đầu của mảnh vườn là :
\(18x28=504\left(m^2\right)\)