Một cốc nước có độ cao là 12cm Nước có trọng lượng riêng kà 10000N/m3 Tính áp suất của nước tác dụng lên 1 điểm cách đáy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:
6x² + 3x - 5 = 3x(2x + 1) - 5
Để M là số nguyên thì (6x² + 3x - 5) ⋮ (2x + 1)
⇒ 5 ⋮ (2x + 1)
⇒ 2x + 1 ∈ Ư(5) = {-5; -1; 1; 5}
⇒ 2x ∈ {-6; -2; 0; 4}
⇒ x ∈ {-3; -1; 0; 2}
Vậy x ∈ {-3; -1; 0; 2} thì M là số nguyên

a) Số sản phẩm công ty sản xuất trong một ngày theo kế hoạch:
10000/x (sản phẩm)
b) Số sản phẩm công ty thực tế đã làm được trong một ngày:
10080/(x - 1) (sản phẩm)
c) Số sản phẩm theo kế hoạch mỗi ngày phải làm:
10000/25 = 400 (sản phẩm)
Số sản phẩm thực tế làm mỗi ngày:
10080/(25 - 1) = 420 (sản phẩm)
Số sản phẩm làm thêm mỗi ngày:
420 - 400 = 20 (sản phẩm)
Bổ sung:
c, Số sản phẩm công ty làm thêm trong một ngày biểu thị theo \(x\) là:
\(\dfrac{10080}{x-1}\) - \(\dfrac{10000}{x}\) = \(\dfrac{80x+10000}{x\left(x-1\right)}\) (sản phẩm)

\(\dfrac{6}{x^2-3x}\) = \(\dfrac{A}{x}\) + \(\dfrac{B}{x-3}\) (nếu đúng với mọi \(x\) ≠0; 3 thì làm như sau)
Đkxđ: \(\left\{{}\begin{matrix}x^2-3x\ne0\\x\ne0\\x-3\ne0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x\left(x-3\right)\ne0\\x\ne0\\x\ne3\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x\ne0\\x\ne3\end{matrix}\right.\)
\(\dfrac{A}{x}\) + \(\dfrac{B}{x-3}\) = \(\dfrac{A.\left(x-3\right)}{x.\left(x-3\right)}\) + \(\dfrac{B.x}{x\left(x-3\right)}\) = \(\dfrac{Ax-3A+Bx}{x\left(x-3\right)}\)
⇒\(\dfrac{6}{x^2-3x}\) = \(\dfrac{6}{x.\left(x-3\right)}\) = \(\dfrac{Ax-3A+Bx}{x.\left(x-3\right)}\)
⇒ \(\dfrac{6}{x\left(x-3\right)}\) - \(\dfrac{Ax-3A+Bx}{x\left(x-3\right)}\) = 0
\(\dfrac{1}{x\left(x-3\right)}\).[6 - (A\(x\) - 3A + B\(x\))] = 0
⇒ 6 - A\(x\) + 3A - B\(x\) = 0
⇒ - \(x\).( A + B) + 6 + 3A = 0 (1)
(1) đúng với ∀ \(x\) ≠0; 3 ⇔ \(\left\{{}\begin{matrix}A+B=0\\6+3A=0\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}A=-B\\3A=-6\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}A=-B\\A=-6:3\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}B=-A\\A=-2\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}B=2\\A=-2\end{matrix}\right.\)
Vậy A = -2; B = 2
\(\dfrac{6}{x^2-3x}=\dfrac{A}{x}+\dfrac{B}{x-3}\left(x\ne0;x\ne3\right)\)
\(\Leftrightarrow\dfrac{6}{x\left(x-3\right)}=\dfrac{A\left(x-3\right)}{x\left(x-3\right)}+\dfrac{Bx}{x\left(x-3\right)}\)
\(\Leftrightarrow6=A\left(x-3\right)+Bx\)
\(\Leftrightarrow6=Ax-3A+Bx\)
\(\Leftrightarrow0x+6=\left(A+B\right)x-3A\)
\(\Leftrightarrow\left\{{}\begin{matrix}A+B=0\\-3A=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}A=-B\\A=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=2\\A=-2\end{matrix}\right.\)

Bài 3:
a, rút gọn P = \(\dfrac{x^2}{x+1}\) + \(\dfrac{2.\left(x-1\right)}{x}\) + \(\dfrac{x+2}{x^2+x}\) với \(x\ne0;x\ne-1\)
P = \(\dfrac{x^2}{x+1}\) + \(\dfrac{2\left(x-1\right)}{x}\) + \(\dfrac{x+2}{x.\left(x+1\right)}\)
P = \(\dfrac{x^2.x}{\left(x+1\right).x}\) + \(\dfrac{2\left(x-1\right)\left(x+1\right)}{x.\left(x+1\right)}\) + \(\dfrac{x+2}{x\left(x+1\right)}\)
P = \(\dfrac{x^3}{x\left(x+1\right)}\) + \(\dfrac{2\left(x^2-1\right)}{x\left(x+1\right)}\) + \(\dfrac{x+2}{x\left(x+1\right)}\)
P = \(\dfrac{x^3+2x^2-2+x+2}{x.\left(x+1\right)}\)
P = \(\dfrac{x^3+2x^2+x-\left(2-2\right)}{x.\left(x+1\right)}\)
P = \(\dfrac{x^3+2x^2+x}{x.\left(x+1\right)}\)
P = \(\dfrac{x\left(x^2+2x+1\right)}{x.\left(x+1\right)}\)
P = \(\dfrac{x.\left(x+1\right)^2}{x.\left(x+1\right)}\)
P = \(x\) + 1
b, Thay \(x\) = 1 vào biểu thức P = \(x\) + 1 ta có:
P = 1 + 1
P = 2

a) \(A+\dfrac{1}{x+1}=\dfrac{3x+1}{x^2-2x+1}-\dfrac{x+3}{x^2-1}\left(x\ne\pm1\right)\)
\(A=\dfrac{3x+1}{\left(x-1\right)^2}-\dfrac{x+3}{\left(x+1\right)\left(x-1\right)}-\dfrac{1}{x+1}\)
\(A=\dfrac{\left(3x+1\right)\left(x+1\right)}{\left(x-1\right)^2\left(x+1\right)}-\dfrac{\left(x+3\right)\left(x-1\right)}{\left(x-1\right)^2\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)^2\left(x+1\right)}\)
\(A=\dfrac{3x^2+3x+x+1-x^2+x-3x+3-x^2+2x-1}{\left(x-1\right)^2\left(x+1\right)}\)
\(A=\dfrac{x^2+4x+3}{\left(x-1\right)^2\left(x+1\right)}\)
\(A=\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)^2\left(x+1\right)}\)
\(A=\dfrac{x+3}{\left(x-1\right)^2}\)
\(A=\dfrac{x+3}{x^2-2x+1}\)
b) \(\dfrac{4}{x^2+x+1}-P=\dfrac{2}{1-x}+\dfrac{2x^2+4x}{x^3-1}\)
\(P=\dfrac{4}{x^2+x+1}-\dfrac{2}{1-x}-\dfrac{2x^2+4x}{x^3-1}\)
\(P=\dfrac{4}{x^2+x+1}+\dfrac{2}{x-1}-\dfrac{2x^2+4x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{4\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{2x^2+4x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{4x-4+2x^2+2x+2-2x^2-4x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{2x-2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(P=\dfrac{2}{x^2+x+1}\)

a, \(\dfrac{x+3}{3x-3}\) + \(\dfrac{2-x}{4x-4}\)
đkxđ: \(\left\{{}\begin{matrix}3x-3\ne0\\4x-4\ne0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}3.\left(x-1\right)\ne0\\4.\left(x-1\right)\ne0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x-1\ne0\\x-1\ne0\end{matrix}\right.\) ⇒ \(x\) ≠1
A = \(\dfrac{x+3}{3x-3}\) + \(\dfrac{2-x}{4x-4}\)
A = \(\dfrac{x+3}{3.\left(x-1\right)}\) + \(\dfrac{2-x}{4.\left(x-1\right)}\)
A = \(\dfrac{4.\left(x+3\right)}{4.3.\left(x-1\right)}\) + \(\dfrac{3.\left(2-x\right)}{3.4.\left(x-1\right)}\)
A = \(\dfrac{4x+12}{12\left(x-1\right)}\) + \(\dfrac{6-3x}{12\left(x-1\right)}\)
A = \(\dfrac{4x+12+6-3x}{12\left(x-1\right)}\)
A = \(\dfrac{\left(4x-3x\right)+\left(12+6\right)}{12\left(x-1\right)}\)
A = \(\dfrac{x+18}{12.\left(x-1\right)}\)
b, \(\dfrac{3}{x+2}-\dfrac{6}{x-1}\)
Đkxđ: \(\left\{{}\begin{matrix}x+2\ne0\\x-1\ne0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x\ne-2\\x\ne1\end{matrix}\right.\)
B = \(\dfrac{3}{x+2}\) - \(\dfrac{6}{x-1}\)
B = \(\dfrac{3.\left(x-1\right)}{\left(x+2\right)\left(x-1\right)}\) - \(\dfrac{6.\left(x+2\right)}{\left(x-1\right)\left(x+2\right)}\)
B = \(\dfrac{3x-3}{\left(x+2\right)\left(x-1\right)}\) - \(\dfrac{6x+12}{\left(x-1\right)\left(x+2\right)}\)
B = \(\dfrac{3x-3-\left(6x+12\right)}{\left(x+2\right)\left(x-1\right)}\)
B = \(\dfrac{3x-3-6x-12}{\left(x+2\right)\left(x-1\right)}\)
B = \(\dfrac{\left(3x-6x\right)-\left(12+3\right)}{\left(x+2\right)\left(x-1\right)}\)
B = \(\dfrac{-3x-15}{\left(x+2\right)\left(x-1\right)}\)

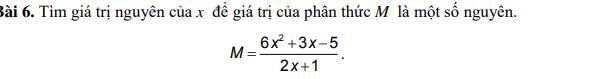


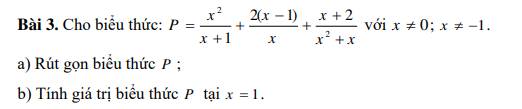


Áp suất nước tác dụng lên một điểm cách đáy:
\(p=d\cdot h=10000\cdot12\cdot10^{-2}=1200N/m^2\)