ai chỉ tui với
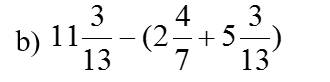
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(42\cdot\left(-45\right)-55\cdot\left(-42\right)\)
\(=-42\cdot45+55\cdot42\)
\(=42\left(55-45\right)=42\cdot10=420\)
b: \(\left(-2-3\right)^2-\left(-2\right)^8:\left(-2\right)^5\)
\(=\left(-5\right)^2-\left(-2\right)^3\)
\(=25-\left(-8\right)=33\)
c: \(\dfrac{1}{5}-\dfrac{-3}{2}+\dfrac{4}{7}-\dfrac{3}{-10}\)
\(=\dfrac{1}{5}+\dfrac{3}{2}+\dfrac{3}{10}+\dfrac{4}{7}\)
\(=\dfrac{2+15+3}{10}+\dfrac{4}{7}=2+\dfrac{4}{7}=\dfrac{18}{7}\)
d: \(\dfrac{3}{22}-\left(\dfrac{7}{15}-\dfrac{-3}{22}\right)+\dfrac{7}{15}-\dfrac{1}{2}\)
\(=\dfrac{3}{22}-\dfrac{7}{15}+\dfrac{3}{22}+\dfrac{7}{15}-\dfrac{1}{2}\)
\(=\dfrac{3}{11}-\dfrac{1}{2}=\dfrac{-5}{22}\)
e: \(6\dfrac{5}{12}:2\dfrac{3}{4}+11\dfrac{1}{4}\cdot\left(\dfrac{1}{3}-\dfrac{1}{5}\right)\)
\(=\dfrac{77}{12}:\dfrac{11}{4}+\dfrac{45}{4}\cdot\dfrac{2}{15}\)
\(=\dfrac{77}{12}\cdot\dfrac{4}{11}+\dfrac{45}{15}\cdot\dfrac{2}{4}\)
\(=\dfrac{7}{3}+\dfrac{3}{2}=\dfrac{23}{6}\)
f: \(\dfrac{-7}{11}\cdot\dfrac{11}{19}+\dfrac{-7}{11}\cdot\dfrac{12}{19}-\dfrac{4}{19}\cdot\dfrac{-7}{11}\)
\(=\dfrac{-7}{11}\left(\dfrac{11}{19}+\dfrac{12}{19}-\dfrac{4}{19}\right)\)
\(=\dfrac{-7}{11}\cdot1=-\dfrac{7}{11}\)

C = \(\dfrac{2}{3.5}\) + \(\dfrac{2}{5.7}\) + ... + \(\dfrac{2}{99.101}\)
C = \(\dfrac{1}{3}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{7}\) + ... + \(\dfrac{1}{99}\) - \(\dfrac{1}{101}\)
C = \(\dfrac{1}{3}\) - \(\dfrac{1}{101}\)
C = \(\dfrac{98}{303}\)

Để \(\dfrac{5}{3n+1}\) là số nguyên thì \(5⋮3n+1\)
=>\(3n+1\in\left\{1;-1;5;-5\right\}\)
=>\(3n\in\left\{0;-2;4;-6\right\}\)
=>\(n\in\left\{0;-\dfrac{2}{3};\dfrac{4}{3};-2\right\}\)
mà n nguyên
nên \(n\in\left\{0;-2\right\}\)
Vì tử số là 5, nên mẫu số phải là 1 hoặc 5 (vì 5 chỉ có 2 ước là 1 và 5).
Vậy ta có hai trường hợp:
1) Nếu $3n+1 = 1$ thì $n = 0$.
2) Nếu $3n+1 = 5$ thì $n = \frac{4}{3}$.
Vì $n$ phải là số nguyên, nên giá trị duy nhất của $n$ là $n = 0$.

\(\dfrac{7}{8}\) : \(x\) + \(\dfrac{3}{4}\) = - \(\dfrac{1}{2}\)
\(\dfrac{7}{8}\) : \(x\) = - \(\dfrac{1}{2}\) - \(\dfrac{3}{4}\)
\(\dfrac{7}{8}\) : \(x\) = - \(\dfrac{5}{4}\)
\(x\) = \(\dfrac{7}{8}\) : (- \(\dfrac{5}{4}\))
\(x\) = - \(\dfrac{7}{10}\)

A = \(\dfrac{3n-1}{n+2}\) (n \(\in\) z; n ≠ -2)
A \(\in\) Z ⇔ 3n - 1 ⋮ n + 2
3n + 6 - 7 ⋮ n + 2
3.(n + 2) - 7 ⋮ n + 2
7 ⋮ n + 2
n + 2 \(\in\) Ư(7) = {-7; -1; 1; 7}
Lập bảng ta có:
| n + 2 | -7 | -1 | 1 | 7 |
| n | -9 | -3 | -1 | 5 |
Theo bảng trên ta có:
n \(\in\) {-9; -3; -1; 5}
Kết luận để A = \(\dfrac{3n-1}{n+2}\) là số nguyên thì n \(\in\) {-9; -3; -1; 5}

sau 12 tháng, số tiền bố của Tuấn lấy ra là khoảng 1,072,482.164 đồng, bao gồm cả vốn và lãi.

\(\dfrac{5}{2\cdot4}+\dfrac{5}{4\cdot6}+...+\dfrac{5}{48\cdot50}\)
\(=\dfrac{5}{2}\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{48\cdot50}\right)\)
\(=\dfrac{5}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{48}-\dfrac{1}{50}\right)\)
\(=\dfrac{5}{2}\left(\dfrac{1}{2}-\dfrac{1}{50}\right)=\dfrac{5}{2}\cdot\dfrac{24}{50}=\dfrac{120}{100}=\dfrac{6}{5}\)

Tìm x :
2/2.4 + 2/4.6 +....+ 2/x(x+2) = 4/9
=> 1/2 - 1/4 + 1/4 - 1/6 + ...+ 1/x - 1/(x + 2) = 4/9
=> 1/2 - 1/(x + 2) = 4/9
=> 1/(x + 2) = 1/18
=> x + 2 = 18
=> x = 16
ĐKXĐ: x ≠ 0; x ≠ -2
2/(2.4) + 2/(4.6) + ... + 2/[x(x + 2)] = 4/9
1/2 - 1/4 + 1/4 - 1/6 + ... + 1/x - 1/(x + 2) = 4/9
1/2 - 1/(x + 2) = 4/9
9(x + 2) - 18 = 4.2(x + 2)
9x + 18 - 18 = 8x + 16
9x - 8x = 16
x = 16 (nhận)
Vậy x = 16
Lời giải:
$11\frac{3}{13}-(2\frac{4}{7}+5\frac{3}{13})=11\frac{3}{13}-5\frac{3}{13}-2\frac{4}{7}$
$=6-2\frac{4}{7}=4-\frac{4}{7}=\frac{24}{7}$
b) 146/13 - ( 18/7 + 68/13)
= 146/13 - 710/91
= 24/7 :))