Hai đội công nhân cùng làm chung 1 công việc trong 12 ngày thì xong . Khi làm chung được 8 ngày thì đội 1 được điều động đi làm việc khác ,đội thứ 2 tiếp tục làm việc với năng suất gấp đôi , do đó đội 2 đã hoàn thành phần việc còn lại trong 8 ngày tiếp theo . Hỏi với năng suất ban đầu thì mỗi đội làm một mình sẽ hoàn thành công việc đó trong bao lâu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Áp dụng BĐT AM-GM ta có:
$P=\sum \frac{1}{(x^2+y^2)+(y^2+1)+2}\leq \sum \frac{1}{2xy+2y+2}$
$=\frac{1}{2}\sum \frac{1}{xy+y+1}$
$=\frac{1}{2}(\frac{1}{xy+y+1}+\frac{1}{yz+z+1}+\frac{1}{xz+x+1})$
$=\frac{1}{2}(\frac{z}{xyz+yz+z}+\frac{1}{yz+z+1}+\frac{yz}{xzyz+xyz+yz})$
$=\frac{1}{2}(\frac{z}{1+yz+z}+\frac{1}{yz+z+1}+\frac{yz}{z+1+yz})$
$=\frac{1}{2}.\frac{1+yz+z}{1+yz+z}=\frac{1}{2}$


a, \(C_2H_4+3O_2\underrightarrow{t^o}2CO_2+2H_2O\)
\(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_{3\downarrow}+H_2O\)
b, Ta có: \(n_{C_2H_4}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
Theo PT: \(n_{O_2}=3n_{C_2H_4}=0,3\left(mol\right)\Rightarrow V_{O_2}0,3.22,4=6,72\left(l\right)\)
c, Theo PT: \(n_{CaCO_3}=n_{CO_2}=2n_{C_2H_4}=0,2\left(mol\right)\Rightarrow m_{CaCO_3}=0,2.100=20\left(g\right)\)

ĐKXĐ : \(0\le x\le1\)
Đặt \(\sqrt{x}=a;\sqrt{1-x}=b\left(a;b\ge0\right)\)
Khi đó ta được a2 + b2 = 1 (1)
Lại có phương trình ban đầu trở thành
\(\dfrac{2a^3}{a+b}+ab=1\) (2)
Từ (1) ; (2) ta được \(\dfrac{2a^3}{a+b}+ab=a^2+b^2\)
\(\Leftrightarrow2a^3=\left(a+b\right).\left(a^2-ab+b^2\right)\)
\(\Leftrightarrow a^3=b^3\Leftrightarrow a=b\)
Khi đó \(\sqrt{x}=\sqrt{1-x}\Leftrightarrow x=1-x\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
Vậy tập nghiệm \(S=\left\{\dfrac{1}{2}\right\}\)

ĐK: \(\left\{{}\begin{matrix}x\ne-y\\y\ge\dfrac{3}{2}\end{matrix}\right.\).
\(\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}=1\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-1=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-\dfrac{x+y}{x+y}=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y+3-x-y=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y+3=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-\left(2y-3\right)=0\\2x-\sqrt{2y-3}=0\end{matrix}\right..\)
Đặt a = x, b = \(\sqrt{2y-3}\).
Hệ phương trình trở thành: \(\left\{{}\begin{matrix}a-b^2=0\\2a-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\2b^2-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\b\left(2b-1\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}a=0\\a=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y-3=\dfrac{1}{4}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y=\dfrac{13}{4}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\y=\dfrac{13}{8}\end{matrix}\right.\end{matrix}\right..\)
Vậy hệ phương trình có nghiệm (x;y) \(\in\) \(\left\{\left(0;\dfrac{3}{2}\right),\left(\dfrac{1}{4};\dfrac{13}{8}\right)\right\}\).
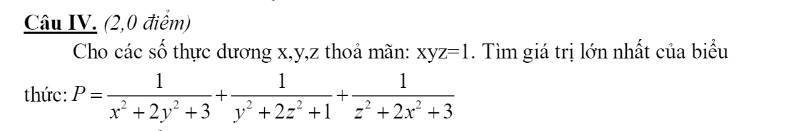
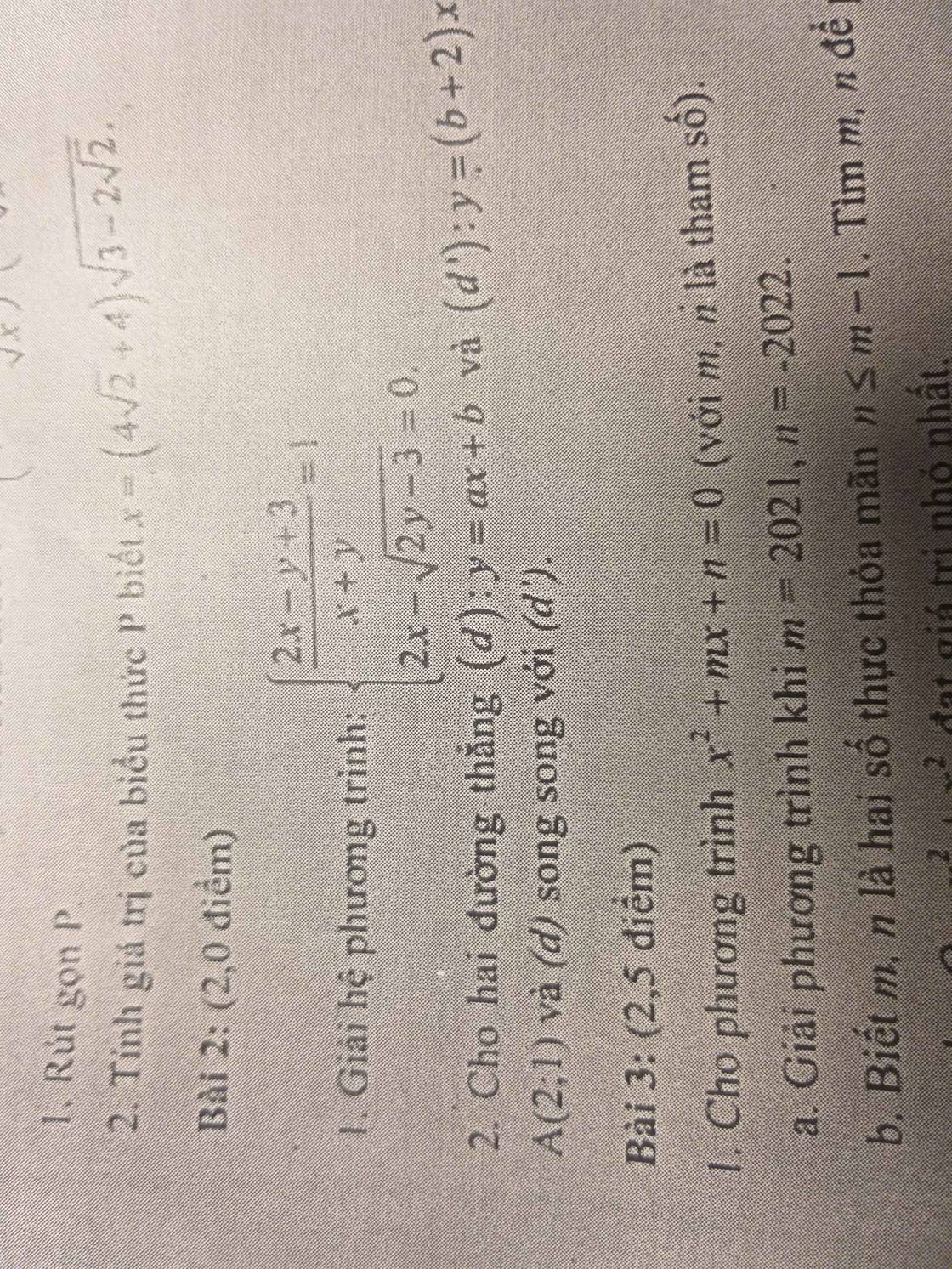
 câu này lỗi đk
câu này lỗi đk