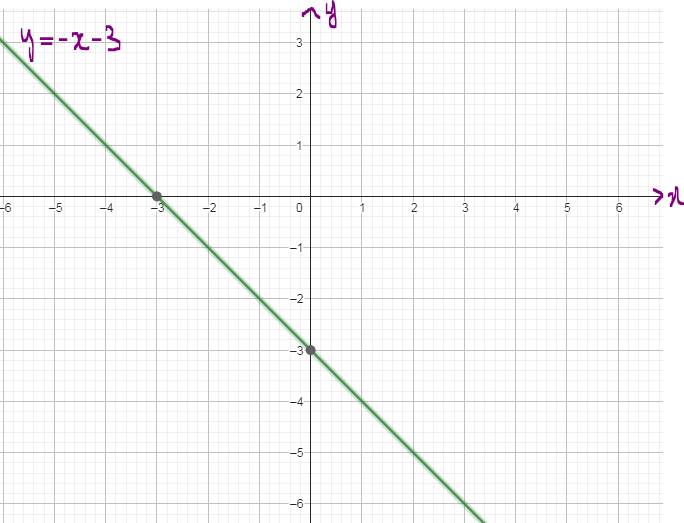
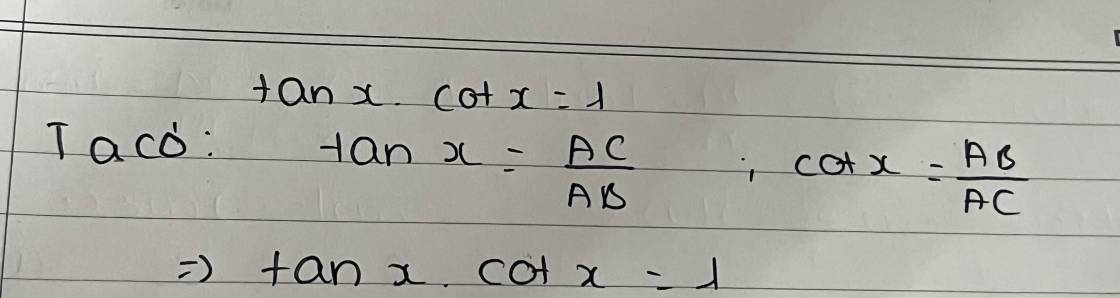(căn x-1) +(căn x^2 -3x+2)+(x-2)nhân(căn x-1/x-2)=2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
UN
0
NL
2
2 tháng 10 2023
Các kì | Những diễn biến cơ bản của $NST$ |
| Kì đầu I | - Các $NST$ kép xoắn và co ngắn. - Các $NST$ kép trong cặp tương đồng tiếp hợp, bắt chéo. |
| Kì giữa I | - Các $NST$ kép trong cặp tương đồng tách nhau ra. - Xếp thành $2$ hàng trên mặt phẳng xích đạo. |
| Kì sau I | - Các $NST$ kép trong cặp tương đồng phân li về $2$ cực của tế bào. |
| Kì cuối I | - Hình thành $2$ tế bào con có bộ $NST$ là $n$ $kép.$ |
| Kết quả | - Từ $1$ tế bào mẹ $2n$ sau giảm phân I tạo ra $2$ tế bào con có bộ $NST$ $n$ $kép$ |
3 tháng 10 2023
Ta có với x,y,z >0 thì:\(\dfrac{x^2}{\sqrt{1-x^2}}=\dfrac{x^3}{x\sqrt{1-x^2}}\)
Bất đẳng thức Cô si ta có:
\(x\sqrt{1-x^2}\le\dfrac{x^2+1-x^2}{2}=\dfrac{1}{2}\\ \Rightarrow\dfrac{1}{x\sqrt{1-x^2}}\ge2\\ \Rightarrow\dfrac{x^3}{x\sqrt{1-x^2}}\ge2x^3\Leftrightarrow\dfrac{x^2}{\sqrt{1-x^2}}\ge2x^3\)
Tương tự: \(\dfrac{y^2}{\sqrt{1-y^2}}\ge2y^3;\dfrac{z^2}{\sqrt{1-z^2}}\ge2z^3\)
Từ đó ta có:\(\dfrac{x^2}{\sqrt{1-x^2}}+\dfrac{y^2}{\sqrt{1-y^2}}+\dfrac{z^2}{\sqrt{1-z^2}}\ge2\left(x^3+y^3+z^3\right)=2\left(dpcm\right)\)
2 tháng 10 2023
\(a,\) Số tế bào tạo ra sau nguyên phân là: \(10.2^4=160\left(tb\right)\)
- Sau giảm phân số tế bào sinh trứng là: \(160\)
\(b,\) Số giao tử cái là: \(2n=8\)
\(c,\) Số thể cực tạo ra: \(160.3=480\)
\(d,\) Số NST tiêu biến cùng các thể cực: $n.480=1920(NST)$
