\(\sqrt{2-\sqrt{3}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài này chỉ tìm được GTLN thôi nhé bạn.
Ta thấy \(A=-\dfrac{1}{3}x^2+2x\)
\(A=-\dfrac{1}{3}\left(x^2-6x\right)\)
\(A=-\dfrac{1}{3}\left(x^2-6x+9\right)+3\)
\(A=-\dfrac{1}{3}\left(x-3\right)^2+3\)
Vì \(\left(x-3\right)^2\ge0\) nên \(A\le3\) (dấu "=" xảy ra khi \(x-3=0\Leftrightarrow x=3\)). Như vậy GTLN của A là 3, đạt được khi \(x=3\).

\(\sqrt{x^2-6x+9}+x=11\); (ĐKXĐ\(\forall x\in R\))
<=> \(\sqrt{x^2-6x+9}=11-x\)
<=> \(\sqrt{\left(x-3\right)^2}=11-x\)
<=> \(|x-3|=11-x\)
<=> \(\left[{}\begin{matrix}x-3=11-x\\x-3=-11+x\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}2x=14\\0x=-8\left(vô\right)lí\left(\right)\end{matrix}\right.\)
<=> x=7 (thỏa mãn ĐKXĐ)
Vậy phương trình có nghiệm là x=7

Bạn sửa lại đề bài nhé. Tam giác ABC vuông tại C (nghĩa là \(\widehat{C}=90^o\)) thì \(\tan C\) làm sao bằng 0,5 được vậy bạn? (thực ra \(\tan C\) thậm chí còn không xác định nữa)

Từ B dựng đường thẳng vuông góc với AC cắt AC tại H
Xét tg vuông ABH có
\(\widehat{ABH}=90^o-\widehat{A}=90^o-60^o=30^o\)
\(\Rightarrow AH=\dfrac{AB}{2}=\dfrac{3}{2}=1,5cm\) (trong tg vuông cạnh đối diện góc 30 độ bằng nửa cạnh huyền)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-1,5^2}\)
Xét tg vuông BCH
\(\widehat{ACB}=30^o\)
=> \(BH=\dfrac{BC}{2}\Rightarrow BC=2.BH\) (lý do như trên)
Bạn tự thay số và tính nốt nhé
Xin lỗi mình nhầm từ chô \(\widehat{ACB}=30^o\)
Ta có
\(CH=AC-AH\)
Xét tg vuông BCH
\(BC=\sqrt{BH^2+CH^2}\)

\(\sqrt{3x^2-9x+1}=x-2\) (ĐK: \(x>2\) )
\(\Leftrightarrow3x^2-9x+1=\left(x-2\right)^2\)
\(\Leftrightarrow3x^2-9x+1=x^2-4x+4\)
\(\Leftrightarrow3x^2-9x+1-x^2+4x-4=0\)
\(\Leftrightarrow2x^2-5x-3=0\)
\(\Rightarrow\Delta=\left(-5\right)^2-4\cdot2\cdot\left(-3\right)=49>0\)
Vậy pt có 2 nghiệm:
\(\left\{{}\begin{matrix}x_1=\dfrac{-\left(-5\right)+\sqrt{49}}{2\cdot2}=3\\x_2=\dfrac{-\left(-5\right)-\sqrt{49}}{2\cdot2}=-\dfrac{1}{2}\left(ktm\right)\end{matrix}\right.\)
Vậy: \(S=\left\{3\right\}\)

\(e,\dfrac{\sqrt{4x-1}}{\sqrt{7-2x}-2}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}4x-1\ge0\\7-2x\ne4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{4}\\x\ne-\dfrac{3}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{1}{4}\)
\(d,\dfrac{\sqrt{2x-1}}{\sqrt{2x+17}+1}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}2x-1\ge0\\2x+17\ge0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{2}\\x\ge-\dfrac{17}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{1}{2}\)
\(b,c,\dfrac{3}{\sqrt{2x-17}}\) có nghĩa \(\Leftrightarrow2x-17>0\Leftrightarrow x>\dfrac{17}{2}\)
\(a,\sqrt{2-5x}\) có nghĩa \(\Leftrightarrow2-5x\ge0\Leftrightarrow x\le\dfrac{2}{5}\)

Chiều dài hình chữ nhật là:
\(\sqrt{5^2-1^2}=5\left(m\right)\)
Diện tích hình chữ nhật là:
\(5\cdot1=5\left(m^2\right)\)
Đáp số: \(5m^2\)
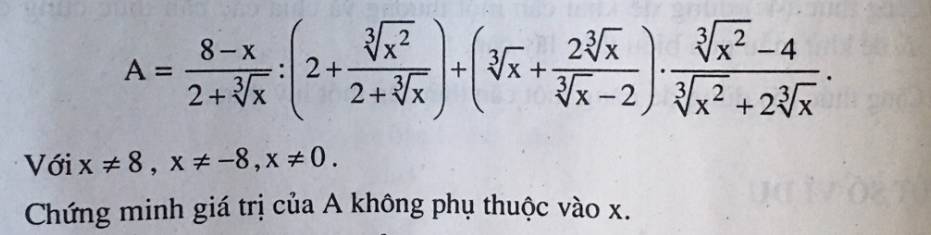
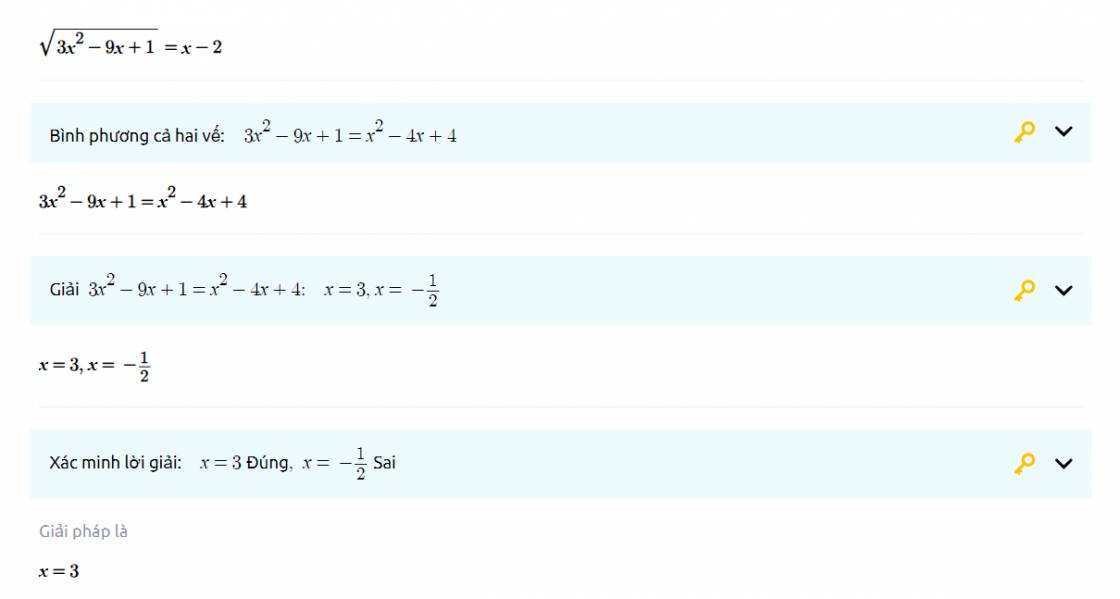
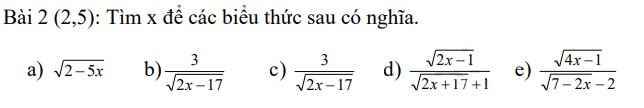
\(\sqrt{2-\sqrt{3}}\)
= \(\dfrac{\sqrt{2}.\sqrt{2-\sqrt{3}}}{\sqrt{2}}\)
= \(\dfrac{\sqrt{4-2\sqrt{3}}}{\sqrt{2}}\)
= \(\dfrac{\sqrt{3-2\sqrt{3}+1}}{\sqrt{2}}\)
= \(\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}}\)
= \(\dfrac{|\sqrt{3}-1|}{\sqrt{2}}\)
= \(\dfrac{\sqrt{3}-1}{\sqrt{2}}\)
= \(\dfrac{\sqrt{2}.\left(\sqrt{3}-1\right)}{2}\)
= \(\dfrac{\sqrt{6}-\sqrt{2}}{2}\)