will you go out if it's sunny on sunday
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: A(x)+B(x)
\(=-3x^3+5x^2+4x+1+3x^3+6x^2-8x+9\)
\(=11x^2-4x+10\)
A(x)-B(x)
\(=-3x^3+5x^2+4x+1-3x^3-6x^2+8x-9\)
\(=-6x^3-x^2+12x-8\)
b: C(x)+D(x)
\(=-x^3+5x^2+5x-\dfrac{3}{4}+4x^3-5x^2-3x-\dfrac{1}{4}\)
\(=3x^3+2x-1\)
C(x)-D(x)
\(=-x^3+5x^2+5x-\dfrac{3}{4}-4x^3+5x^2+3x+\dfrac{1}{4}\)
\(=-5x^3+10x^2+8x-\dfrac{1}{2}\)
c: E(x)+F(x)
\(=3x^3+7x^2+5x-8+3x^3+7x^2-9x+1\)
\(=6x^3+14x^2-4x-7\)
E(x)-F(x)
\(=3x^3+7x^2+5x-8-3x^3-7x^2+9x-1\)
\(=14x-9\)
d: G(x)+H(x)
\(=5x^4-6x^3-3x^2-2x+8+x^4+3x^2-3x-5\)
\(=6x^4-6x^3-5x+3\)
G(x)-H(x)
\(=5x^4-6x^3-3x^2-2x+8-x^4-3x^2+3x+5\)
\(=4x^4-6x^3-6x^2+x+13\)
e: I(x)+J(x)
\(=5x^4-2x^3-6x^2+7x+6+2x^3+3x^2-7x-5\)
\(=5x^4-3x^2+1\)
I(x)-J(x)
\(=5x^4-2x^3-6x^2+7x+6-2x^3-3x^2+7x+5\)
\(=5x^4-4x^3-9x^2+14x+11\)
f: K(x)+L(x)
\(=4x^4+3x^3+5x^2-2x+6-4x^4-3x^3-4x^2+2x-9\)
\(=x^2-3\)
K(x)-L(x)
\(=4x^4+3x^3+5x^2-2x+6+4x^4+3x^3+4x^2-2x+9\)
\(=8x^4+6x^3+9x^2-4x+15\)
g: M(x)+N(x)
\(=-5x^4+4x^3-5x^2-\dfrac{1}{2}x-19+6x^4-4x^3+3x^2+\dfrac{1}{2}x-20\)
\(=x^4-2x^2-39\)
M(x)-N(x)
\(=-5x^4+4x^3-5x^2-\dfrac{1}{2}x-19-6x^4+4x^3-3x^2-\dfrac{1}{2}x+20\)
\(=-11x^4+8x^3-8x^2-x+1\)
h:
\(O\left(x\right)=x^5+x^3-4x-x^5+3x+7\)
\(=\left(x^5-x^5\right)+x^3+\left(-4x+3x\right)+7\)
\(=x^3-x+7\)
\(P\left(x\right)=3x^2-x^3+8x-3x^2-14\)
\(=-x^3+\left(3x^2-3x^2\right)+8x-14=-x^3+8x-14\)
O(x)+P(x)
\(=x^3-x+7-x^3+8x-14\)
\(=7x-7\)
O(x)-P(x)
\(=x^3-x+7+x^3-8x+14\)
\(=2x^3-9x+21\)

Lời giải:
Ta thấy:
$x^4\geq 0; x^2\geq 0$ với mọi $x$
$\Rightarrow Q(x)=x^4+3x^2+1\geq 1>0$ với mọi $x$
$\RIghtarrow Q(x)$ không có nghiệm với mọi $x$

Lời giải:
a. Vì $P(x)$ có nghiệm $x=-1$ nên:
$P(-1)=0$
$\Leftrightarrow m(-1)^2+2m(-1)-3=0$
$\Leftrightarrow m-2m-3=0$
$\Leftrightarrow -m-3=0\Leftrightarrow m=-3$
b.
Có:
$P(-1)=a(-1)^2+b(-1)+c=a-b+c$
$P(-2)=a(-2)^2+b(-2)+c=4a-2b+c$
$\Rightarrow P(-1)+P(-2)=5a-3b+2c=0$
$\Rightarrow P(-1)=-P(-2)$
$\Rightarrow P(-1)P(-2)=-P(-2)P(-2)=-P^2(-2)\leq 0$ (đpcm)

trong số các danh nhân văn hóa thời Lê sơ,em ấn tượng nhất với Nguyễn Trãi.Nguyễn trãi:
+ Nguyễn Trãi không những là một nhà chính trị, quân sự tài ba, một anh hùng dân tộc mà còn là một danh nhân văn hoá thế giới.
+ Ông có nhiều tác phẩm có giá trị lớn về văn học, sử học, địa lí học như Quân trung từ mệnh tập, Bình Ngô đại cáo, Chí Linh sơn phú, Quốc âm thi tập, Dư địa chí...
+ Tư tưởng của ông tiêu biểu cho tư tưởng của thời đại. cả cuộc đời của Nguyễn Trãi, khi đánh giặc cũng như khi xây dựng đất nước hoặc sáng tác thơ văn, ông luôn nêu cao lòng nhân nghĩa, yêu nước, thương dân
có đúng ko cô

a)3-2-1
b)Do nhà Hồ ko có đường lối kháng chiến đúng đắn,chủ yếu dựa vào thành lũy,nặng nề về phòng ngữ bị động và rút lui cố thủ

Trong hình học Euclid, một tam giác thường được xác định bởi ba cạnh và ba góc. Để một tam giác tồn tại, ta cần biết điều kiện cho ba cạnh và ba góc. Trong trường hợp bạn đề cập, nếu ta có một cạnh là góc vuông và một góc nhọn không kề cạnh với góc vuông đó, thì sẽ xảy ra mâu thuẫn.
Vì trong một tam giác, tổng các góc bằng 180 độ, và trong một tam giác vuông, một góc là 90 độ. Nếu một góc khác không kề với góc vuông, nó sẽ phải nằm ở phần còn lại của tam giác, tức là từ 180 độ trừ đi 90 độ, tức là 90 độ. Nhưng điều này không thể xảy ra vì trong tam giác, không thể có góc nào lớn hơn 90 độ.
Vậy nên, một tam giác với một cạnh là góc vuông và một góc nhọn không kề cạnh với nó không thể tồn tại trong hình học Euclid.

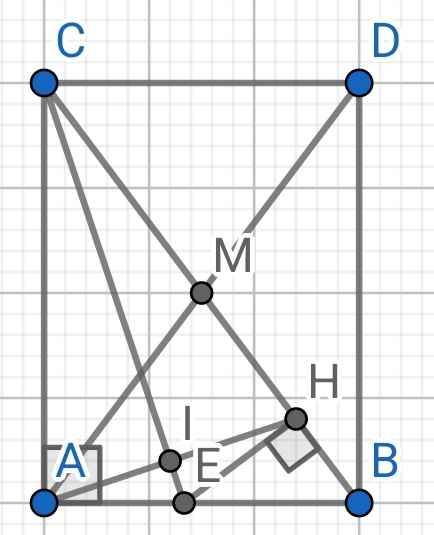
a) ∆ABC vuông tại A (gt)
⇒ ∠ABC + ∠BCA = 90⁰ (hai góc nhọn trong tam giác vuông phụ nhau)
b) Do CE là đường phân giác của ∆ABC (gt)
⇒ CE là tia phân giác của ∠ACB
⇒ ∠ACE = ∠BCE
⇒ ∠ACE = ∠HCE
Xét hai tam giác vuông: ∆ACE và ∆HCE có:
CE là cạnh chung
∠ACE = ∠HCE (cmt)
⇒ ∆ACE = ∆HCE (cạnh huyền - góc nhọn)
⇒ AC = HC (hai cạnh tương ứng)
c) Do ∆ACE = ∆HCE (cmt)
⇒ AE = HE (hai cạnh tương ứng)
⇒ E nằm trên đường trung trực của AH (1)
Do AC = HC (cmt)
⇒ C nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ CE là đường trung trực của AH
Mà I là giao điểm của AH và CE (gt)
⇒ I là trung điểm của AH
⇒ IA = IH
d) Trên tia đối của tia MA lấy điểm D sao cho AM = DM
⇒ M là trung điểm của AD
Do M là trung điểm của BC (gt)
⇒ BM = CM
Xét ∆ABM và ∆DCM có:
AM = DM
∠AMB = ∠DMC (đối đỉnh)
BM = CM (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
⇒ ∠BAM = ∠CDM (hai góc tương ứng)
Mà ∠BAM và ∠CDM là hai góc so le trong
⇒ AB // CD
Mà AB ⊥ AC (∆ABC vuông tại A)
⇒ CD ⊥ AC
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABD và ∆CDB có:
AB = CD (cmt)
DB là cạnh chung
⇒ ∆ABD = ∆CDB (hai cạnh góc vuông)
⇒ AD = BC (hai cạnh tương ứng)
Mà M là trung điểm của AD (cmt)
⇒ AD = 2AM
⇒ BC = 2AM


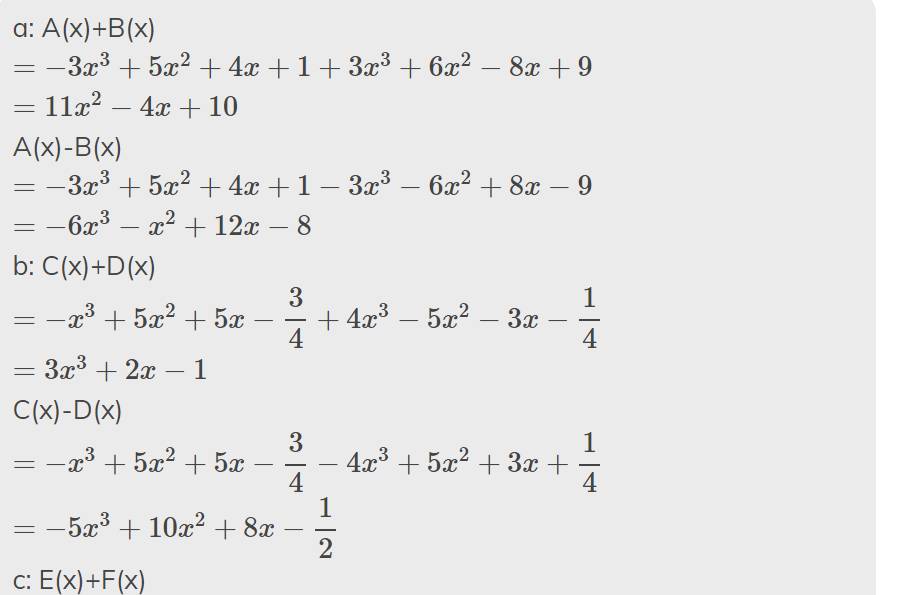

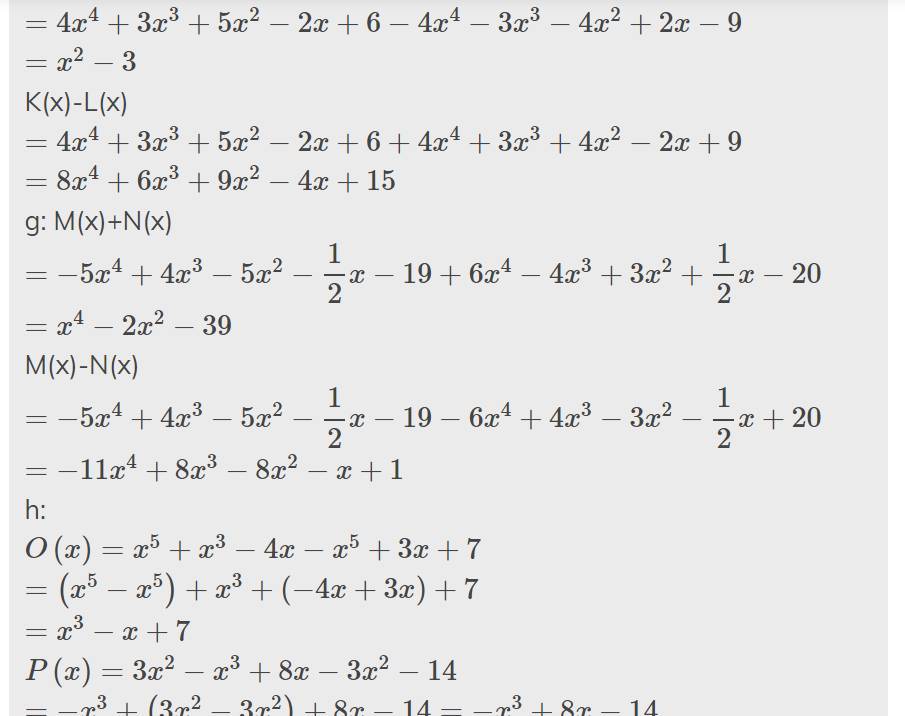
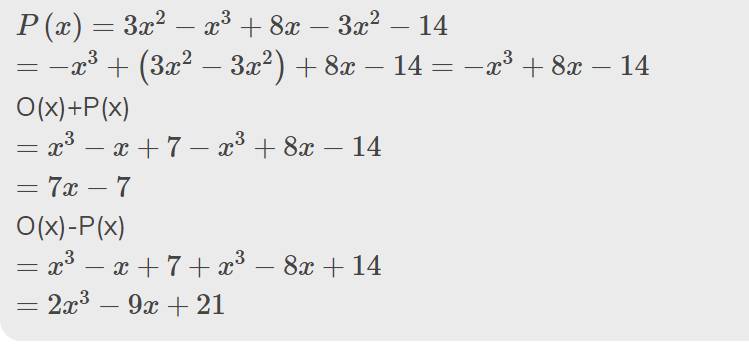
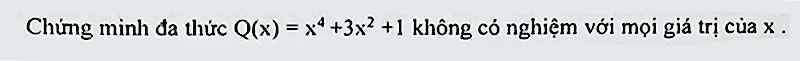
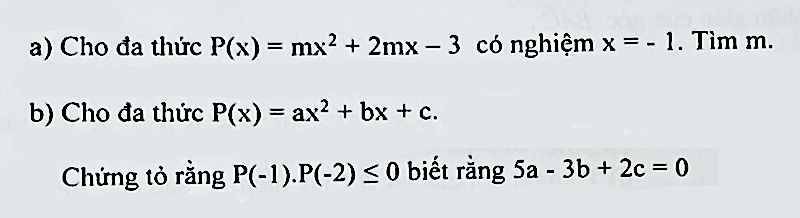
Yes