Tìm x:
(7x-9)(8x+5)(-12x+5)(4x-1)=(3x-5)(8x+7)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{600}{x}+\dfrac{600}{x+30}=1\left(ĐKXĐ:x\ne0,x\ne-30\right)\)
PT < = > 600 ( x + 30 ) + 600x = x( x + 30 )
<=> 600x + 18000 + 600x = x2 + 30x
<=> x2 - 1170 - 18000 = 0
Pt này giải delta ra nghiệm xấu nhé em xem lại đề bài xem có sai chỗ nào k?

1)
a) \(\left(x+2\right)^2-\left(x-2\right)\left(x+2\right)\)
\(=\left(x+2\right)\left[\left(x+2\right)-\left(x-2\right)\right]\)
\(=\left(x+2\right)\left(x+2-x+2\right)\)
\(=4\left(x+2\right)\)
b) \(x+2x^2+2x^3\)
\(=x\left(2x+2x^2+1\right)\)
1) a. \(\left(x+2\right)\left(x+2-x+2\right)=4\left(x+2\right)\)
b. \(x\left(1+2x+2x^2\right)\)
2) a. \(=x^2-4-\left(x^2+4x+3\right)=x^2-4-x^2-4x-3=-4x-7\)
b. Áp dụng dạng \(\left(a+b\right)^2=a^2+b^2+2ab\)
\(\left(2x+1\right)^2+\left(3x-1\right)^2+2\left(2x+1\right)\left(3x-1\right)\)
\(=\left(2x+1+3x-1\right)^2=\left(5x\right)^2=25x^2\)

Bài 1:
a) Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC,OCD và ODA.
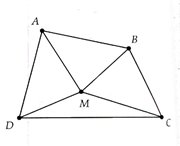
b) Chứng minh tổng hai đường chéo lớn hơn nửa chu vi tứ giác sử dụng kết quả của a).
Chứng minh tổng hai đường chéo nhỏ hơn chu vi tứ giác sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác ABC, ADC, ABD và CBD
Bài 3:
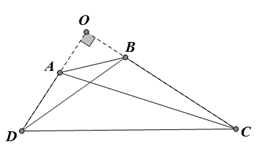
Gọi O là giao điểm AD và BC.
Ta có ˆC+⌢D=900�^+�⏜=900 nên ˆO=900�^=900
Áp dụng định lí Py – ta – go,
Ta có
AC2=OA2+OC2.��2=��2+��2.
BD2=OB2+OD2��2=��2+��2
Nên AC2+BD2=(OA2+OB2)+(OC2+OD2)=AB2+CD2
Bài 1: 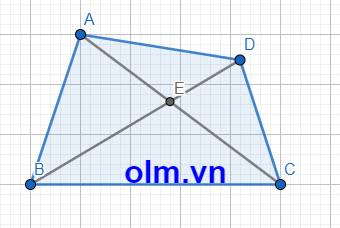
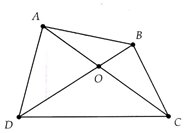
Gọi E là giao điểm của hai đường chéo AC và BD
Xét tam giác AEB ta có: AE + BE > AB (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét tam giác DEC ta có: DE + CE > DC (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AE + BE + DE + CE > AB + DC
(AE + CE) + (BE + DE) > AB + DC
AC + BD > AB + DC
Tương tự ta có AC + BD > AD + BC
Kết luận: Trong một tứ giác tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối.
Nửa chu vi của tứ giác ABCD là: \(\dfrac{AB+BC+CD+DA}{2}\)
Theo chứng minh trên ta có:
\(\dfrac{AB+BC+CD+DA}{2}\)< \(\dfrac{\left(AB+CD\right)\times2}{2}\) = AB + CD (1)
Vì trong một tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại nên ta có:
AB + AD > BD
AB + BC > AC
BC + CD > BD
CD + AD > AC
Cộng vế với vế ta có:
(AB + BC + CD + DA)\(\times\)2 > (BD + AC ) \(\times\) 2
⇒AB + BC + CD + DA > BD + AC (2)
Kết hợp (1) và (2) ta có:
Tổng hai đường chéo của tứ giác lớn hơn nửa chu vi của tứ giác nhưng nhỏ hơn chu vi của tứ giác

\(\dfrac{A}{1}=\dfrac{B}{2}=\dfrac{C}{3}=\dfrac{D}{4}=\dfrac{A+B+C+D}{1+2+3+4}=\dfrac{360}{10}=36\)
\(\Rightarrow A=36^0;B=36.2=72^0;C=36.3=108^0;D=36.4=144^0\)

\(a+b+c=1\)
\(\Leftrightarrow\left(a+b+c\right)^3=1\)
\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)=1\)
\(\Leftrightarrow1+3\left(a+b\right)\left(b+c\right)\left(c+a\right)=1\)'
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=0\\b+c=0\\c+a=0\end{matrix}\right.\)
Không mất tính tổng quát, giả sử \(a+b=0\), các trường hợp còn lại làm tương tự.
Khi đó từ \(a+b+c=1\) suy ra \(c=1\) (thỏa mãn). Thế thì \(T=0^{2023}+0^{2023}+1^{2023}=1\).
Như vậy \(T=1\)

A B C D O M N P Q
a/
Ta có
MN//AB (gt)
AD//BC=> AM//BN
=> AMNB là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có
AB//CD => AP//CQ mà AP = CQ (gt) => APCQ là hbh (Tứ giác có cặp cạnh đối // và = nhau là hbh)
b/
Xét hbh ABCD
OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Xét hbh APCQ có
IA=IC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> \(I\equiv O\) (đều là trung điểm AC) => M; N; I thẳng hàng
c/ Do \(I\equiv O\) (cmt) => AC; MN; PQ đồng quy tại O