(0,5 điểm) Hình vẽ mô tả mặt cắt của một chi tiết máy ép nhựa có dạng ở giữa là nửa hình vành khuyên giới hạn bởi hai nửa đường tròn ($O; 15$ cm), ($O; 10$ cm) và hai đầu là hai hình chữ nhật có chiều dài $15$ cm, chiều rộng $5$ cm.
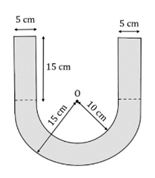
Tính diện tích mặt cắt của chi tiết máy ép nhựa đó (làm tròn kết quả đến hàng phần trăm của centimét vuông).