I. Sơ đồ khảo sát hàm số 1. Tập xác định + Phân thức: mẫu số khác 0 0
+ Căn thức: biểu thức trong căn không âm;
+ Hàm số lượng giác.
2. Sự biến thiên + Xét chiều biến thiên của hàm số:
Tính đạo hàm y' y ′
Tìm các điểm mà tại đó đạo hàm bằng 0 0
Xét dấu đạo hàm y' y ′
+ Tìm cực trị.
+ Tìm các giới hạn vô cực, các giới hạn tại vô cực và tiệm cận (nếu có).
+ Lập bảng biến thiên.
3. Đồ thị + Tìm giao điểm của đồ thị với các trục tọa độ;
+ Dựa vào các yếu tố ở trên để vẽ đồ thị;
+ Chú ý thêm tính chẵn, lẻ và tính tuần hoàn (nếu có).
II. Khảo sát hàm số bậc ba dạng y=ax^3+bx^2+cx+d y = a x 3 + b x 2 + c x + d (a \ne 0) ( a = 0 ) Ví dụ: Khảo sát hàm số y=-x^3+3x^2-4x+2 y = − x 3 + 3 x 2 − 4 x + 2 1) Tập xác định \mathbb R R
2) Sự biến thiên
+ Chiều biến thiên:
y' = y ′ =
-3x^3+6x^2-4x − 3 x 3 + 6 x 2 − 4 x .
Kiểm tra
Ta có y' = -3(x-1)^2-1 < 0, y ′ = − 3 ( x − 1 ) 2 − 1 < 0 , \forall x \in \mathbb R. ∀ x ∈ R .
Nên hàm số đã cho luôn nghịch biến đồng biến (-\infty;+\infty) ( − ∞ ; + ∞ )
và hàm số không có cực trị có cực tiểu có cực đại
Kiểm tra
+ Giới hạn tại vô cực:
\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\left[-x^3\left(1-\dfrac{3}{x}+\dfrac{4}{x^2}-\dfrac{2}{x^3}\right)\right]=+\infty x → − ∞ lim y = x → − ∞ lim [ − x 3 ( 1 − x 3 + x 2 4 − x 3 2 ) ] = + ∞
\lim\limits_{x\rightarrow+\infty}y= x → + ∞ lim y = + - \infty ∞
Kiểm tra
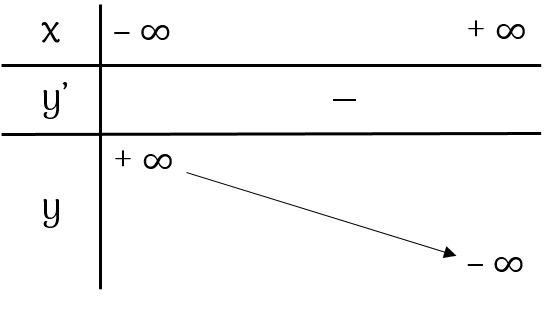
+ Bảng biến thiên
3) Đồ thị
Đồ thị hàm số cắt trục Ox O x (1;0) ( 1 ; 0 )
và cắt trục Oy O y 0 1 2 -1 0 2
Kiểm tra
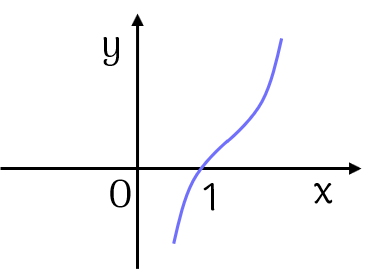
Đồ thị của hàm số đã cho là
Dạng đồ thị các hàm số dạng y=ax^3+bx^2+cx+d y = a x 3 + b x 2 + c x + d (a\ne 0) ( a = 0 )
III. Khảo sát hàm số trùng phương dạng y= ax^4+bx^2+c y = a x 4 + b x 2 + c (a\ne 0) ( a = 0 )
IV. Khảo sát hàm số phân thức dạng y=\dfrac{ax+b}{cx+d} y = c x + d a x + b (cx+d \ne 0; ad-bc \ne 0) ( c x + d = 0 ; a d − b c = 0 )
I. Sơ đồ khảo sát hàm số 1. Tập xác định + Phân thức: mẫu số khác 0 0
+ Căn thức: biểu thức trong căn không âm;
+ Hàm số lượng giác.
2. Sự biến thiên + Xét chiều biến thiên của hàm số:
Tính đạo hàm y' y ′
Tìm các điểm mà tại đó đạo hàm bằng 0 0
Xét dấu đạo hàm y' y ′
+ Tìm cực trị.
+ Tìm các giới hạn vô cực, các giới hạn tại vô cực và tiệm cận (nếu có).
+ Lập bảng biến thiên.
3. Đồ thị + Tìm giao điểm của đồ thị với các trục tọa độ;
+ Dựa vào các yếu tố ở trên để vẽ đồ thị;
+ Chú ý thêm tính chẵn, lẻ và tính tuần hoàn (nếu có).
II. Khảo sát hàm số bậc ba dạng y=ax^3+bx^2+cx+d y = a x 3 + b x 2 + c x + d (a \ne 0) ( a = 0 ) Ví dụ: Khảo sát hàm số y=-x^3+3x^2-4x+2 y = − x 3 + 3 x 2 − 4 x + 2 1) Tập xác định \mathbb R R
2) Sự biến thiên
+ Chiều biến thiên:
y' = y ′ =
-3x^3+6x^2-4x − 3 x 3 + 6 x 2 − 4 x .
Kiểm tra
Ta có y' = -3(x-1)^2-1 < 0, y ′ = − 3 ( x − 1 ) 2 − 1 < 0 , \forall x \in \mathbb R. ∀ x ∈ R .
Nên hàm số đã cho luôn nghịch biến đồng biến (-\infty;+\infty) ( − ∞ ; + ∞ )
và hàm số không có cực trị có cực tiểu có cực đại
Kiểm tra
+ Giới hạn tại vô cực:
\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\left[-x^3\left(1-\dfrac{3}{x}+\dfrac{4}{x^2}-\dfrac{2}{x^3}\right)\right]=+\infty x → − ∞ lim y = x → − ∞ lim [ − x 3 ( 1 − x 3 + x 2 4 − x 3 2 ) ] = + ∞
\lim\limits_{x\rightarrow+\infty}y= x → + ∞ lim y = + - \infty ∞
Kiểm tra
+ Bảng biến thiên
3) Đồ thị
Đồ thị hàm số cắt trục Ox O x (1;0) ( 1 ; 0 )
và cắt trục Oy O y 0 1 2 -1 0 2
Kiểm tra
Đồ thị của hàm số đã cho là
Dạng đồ thị các hàm số dạng y=ax^3+bx^2+cx+d y = a x 3 + b x 2 + c x + d (a\ne 0) ( a = 0 )
III. Khảo sát hàm số trùng phương dạng y= ax^4+bx^2+c y = a x 4 + b x 2 + c (a\ne 0) ( a = 0 )
IV. Khảo sát hàm số phân thức dạng y=\dfrac{ax+b}{cx+d} y = c x + d a x + b (cx+d \ne 0; ad-bc \ne 0) ( c x + d = 0 ; a d − b c = 0 )








.png)
.png)
.png)