
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
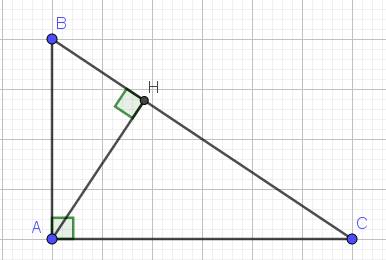
a. Trong tam giác $ABC$ có $AC> AB$, mà $\widehat{B}$ đối diện cạnh $AC$, $\widehat{C}$ đối diện $AB$ nên $\widehat{B}> \widehat{C}$
b. Có:
$\widehat{B}=90^0-\widehat{BAH}=\widehat{HAC}$
$\widehat{C}=90^0-\widehat{HAC}=\widehat{BAH}$
c.
Xét tam giác $ABH$ vuông tại $H$ có $AB$ là cạnh huyền, $AH$ là cạnh góc vuông nên $AB> AH$
Xét tam giác $ACH$ vuông tại $H$ có $AC$ là cạnh huyền, $AH$ là cạnh góc vuông nên $AC> AH$

2x/10=3y/9=4z/8
Theo tính chất dãy tỉnh số bằng nhau ta có:
2x/10=3y/9=4z/8 => 2x+3y+4z/10+9+8 = 54/27 = 2
=> x = 5 x 2 =10
y = 3 x 2 = 6
z = 2 x 2 = 4
Ta có:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{2}\Rightarrow\dfrac{2x}{10}=\dfrac{3y}{9}=\dfrac{4z}{8}\)
Áp dụng tính chấ dãy tỉ số bằng nhau, ta có:
\(\dfrac{2x}{10}=\dfrac{3y}{9}=\dfrac{4z}{8}=\dfrac{2x+3y+4z}{10+9+8}=\dfrac{54}{27}=2\)
Do đó:
\(\dfrac{x}{5}=2\Rightarrow x=5.2=10\)
\(\dfrac{y}{3}=2\Rightarrow y=3.2=6\)
\(\dfrac{z}{2}=2\Rightarrow z=2.2=4\)
Vậy x = 10; y = 6; z = 4.
\(#NqHahh\)

Di chuột vô góc phải Màn hình (vào tên của mình) nhưng đừng vội nhấn.
B2: ấn vào "thông tin tài khoản"
rồi bạn muốn chỉnh gì thì chỉnh.

\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)

xét 2 tam giác AMB và DMC
có AM = DM ( gt )
góc DMC = góc AMB ( 2 góc đối đỉnh )
BM = CM ( M là trung điểm của BC )
=> tam giác AMB = tam giác DMC ( c.g.c ) ( đpcm )
b, xét hai tam giác AMC và DMB
có AM = DM ( gt )
góc DMB = góc AMC ( 2 góc đối đỉnh )
BM = CM ( M là trung điểm của BC )
=> tam giác AMC = ta giác DMB ( c.g.c )
=> góc DBM = góc ACM ( 2 góc tương ứng )
mà 2 góc trên nằm ở vị trí so le trong của 2 đt AC và BD
=> AC // BD ( đpcm )
c, từ b có
tam giác AMC = tam giác DMB ( c.g.c )
=> AC = BD ( 2 cạnh tương ứng )
và góc DBM = góc ACM ( 2 góc tương ứng )
xét hai tam giác AKC và BHD
có góc BHD = góc CKA = 90 độ
AC = BD (cmt)
góc DBM = góc ACM ( cmt )
=> tam giác AKC = tam giác BHD ( cạnh huyền - govs nhọn )
=> BH = CK ( 2 cạnh tương ứng )(đpcm )

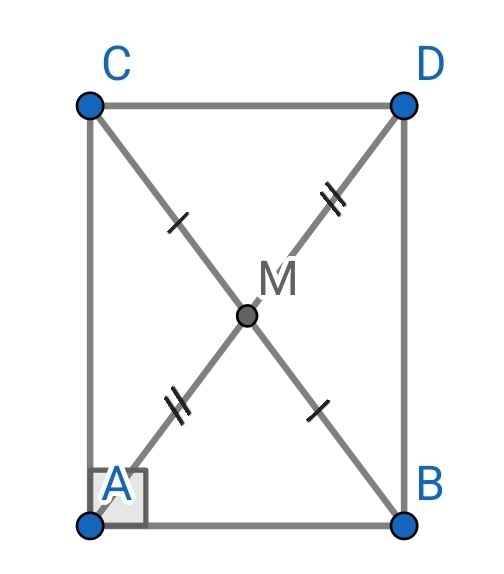 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆MAB và ∆MDC có:
MA = MD (gt)
∠AMB = ∠DMC (đối đỉnh)
MB = MC (cmt)
⇒ ∆MAB = ∆MDC (c-g-c)
b) Do ∆MAB = ∆MDC (cmt)
⇒ ∠MAB = ∠MDC (hai góc tương ứng)
Mà ∠MAB và ∠MDC là hai góc so le trong
⇒ AB // CD
c) Do MA = MD (gt)
⇒ AD = 2AM
Do ∆ABC vuông tại A (gt)
⇒ AB ⊥ AC
Mà AB // CD (cmt)
⇒ CD ⊥ AC
⇒ ∆CDA vuông tại C
Do ∆MAB = ∆MDC (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABC và ∆CDA có:
AC là cạnh chung
AB = CD (cmt)
⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)
⇒ BC = AD (hai cạnh tương ứng)
Mà AD = 2AM (cmt)
⇒ BC = 2AM
d) Xét ∆MAC và ∆MDB có:
MA = MD (gt)
∠AMC = ∠DMB (đối đỉnh)
MC = MB (cmt)
⇒ ∆MAC = ∆MDB (c-g-c)
⇒ ∠MAC = ∠MDB (hai góc tương ứng)
Mà ∠MAC và ∠MDB là hai góc so le trong
⇒ AC // BD
Mà AC ⊥ AB (cmt)
⇒ AB ⊥ BD
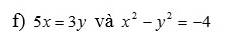
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC