2.5 + 5.8 + ... + 293.296 + 296.299 các bạn giúp mình với nhé ai nhanh mình tick nhe
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề: Chiều rộng là x (m)
Do chiều dài gấp đôi chiều rộng nên chiều dài là 2x (m)
Diện tích hình chữ nhật là:
2x.x = 2x² (m²)

a, Ta có (AC;AB) = ^BAC
tan^BAC = BC/AB = 1 => ^BAC = 450
b, Ta có BD // B'D'
=> (AD';BD) = (AD';B'D') = ^AD'B'
Xét tam giác AD'B' ta có AB' = B'D' = AD'
=> tam giác AD'B' đều => ^AD'B' = 600
c, Ta có BD vuông AC ; BD vuông CC'
=> BD vuông (ACC')
Mà AC' thuộc (ACC') => AC' vuông BD

a/
Xét tg ABI và tg ACI có
AB=AC (cạnh bên tg cân)
\(\widehat{BAH}=\widehat{CAH}\) (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh)
AI chung
=> tg ABI = tg ACI (c.g.c) => IB=IC => tg IBC cân
b/
tg ABI = tg ACI (cmt) \(\Rightarrow\widehat{AIB}=\widehat{AIC}\)
c/ Xét tg IBF và tg ICE có
\(\widehat{BIF}=\widehat{CIE}\) (góc đối đỉnh)
IB=IC (cmt)
tg ABI = tg ACI (cmt) \(\Rightarrow\widehat{ABI}=\widehat{ACI}\)
=> tg IBF = tg ICE => IE=IF
d/
Ta có
IE=IF (cmt) => tg IEF cân tại I
\(\Rightarrow\widehat{IEF}=\widehat{IFE}=\dfrac{180^o-\widehat{FIE}}{2}\) (1)
Xét tg cân IBC có
\(\widehat{IBC}=\widehat{ICB}=\dfrac{180^o-\widehat{BIC}}{2}\) (2)
Mà \(\widehat{FIE}=\widehat{BIC}\) (góc đối đỉnh) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{IFE}=\widehat{ICB}\) Hai góc này nằm ở vị trí so le trong
=> EF//BC
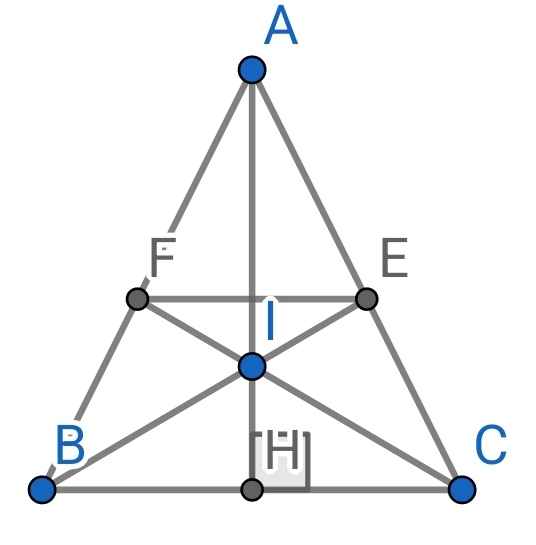 a) ∆ABC cân tại A (gt)
a) ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH cũng là đường trung trực của ∆ABC
⇒ AH là đường trung trực của BC
I ∈ AH (gt)
⇒ IB = IC
⇒ ∆IBC cân tại I
b) Xét ∆AIB và ∆AIC có:
AI là cạnh chung
AB = AC (do ∆ABC cân tại A)
IB = IC (cmt)
⇒ ∆AIB = ∆AIC (c-c-c)
⇒ ∠AIB = ∠AIC (hai góc tương ứng)
c) Do ∆AIB = ∆AIC (cmt)
⇒ ∠ABI = ∠ACI (hai góc tương ứng)
⇒ ∠FBI = ∠ECI
Xét ∆BIF và ∆CIE có:
∠FBI = ∠ECI (cmt)
IB = IC (cmt)
∠FIB = ∠EIC (đối đỉnh)
⇒ ∆BIF = ∆CIE (g-c-g)
⇒ IF = IE (hai cạnh tương ứng)
Hay IE = IF
d) ∆IBC cân tại I (cmt)
IH là đường trung trực của BC (cmt)
⇒ IH cũng là đường phân giác của ∆IBC
⇒ ∠BIH = ∠CIH
Ta có:
∠AIE = ∠BIH (đối đỉnh)
∠AIF = ∠CIH (đối đỉnh)
Mà ∠BIH = ∠CIH (cmt)
⇒ ∠AIE = ∠AIF
Xét ∆AIE và ∆AIF có:
IE = IF (cmt)
∠AIE = ∠AIF (cmt)
AI là cạnh chung
⇒ ∆AIE = ∆AIF (c-g-c)
⇒ AE = AF (hai cạnh tương ứng)
⇒ A nằm trên đường trung trực của EF (1)
Do IE = IF (cmt)
⇒ I nằm trên đường trung trực của EF (2)
Từ (1) và (2) ⇒ AI là đường trung trực của EF
⇒ AI ⊥ EF
⇒ AH ⊥ EF
Mà AH ⊥ BC (gt)
⇒ EF // BC

Thời gian My đạp xe từ nhà đến trường:
4 : 12 = 1/3 (giờ) = 20 (phút)
My đến trường lúc:
6 giờ 50 phút + 20 phút = 7 giờ 10 phút

Vận tốc Kangaroo tính bằng đơn vị m/giây:
54 × 1000 : 3600 = 15 (m/giây)

(98 . 76 - 9898 . 76) + (2001 + 2002 + 2003 + ... + 2017)
= 76.(98 - 9898) + (2017 + 2001) . 17 : 2
= 76.(-9800) + 4018 . 17 : 2
= -744800 + 34153
= -710647

\(\left(x+2y\right)^3-x^2+4y^2\)
\(=\left(x+2y\right)^3-\left(x-2y\right)\left(x+2y\right)\)
\(=\left(x+2y\right)\left[\left(x+2y\right)^2-\left(x-2y\right)\right]\)
\(=\left(x+2y\right)\left(x^2+4xy+4y^2-x+2y\right)\)
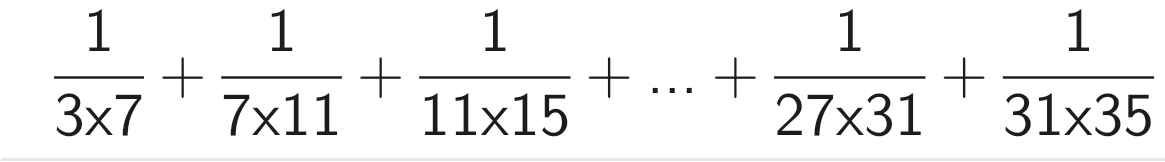
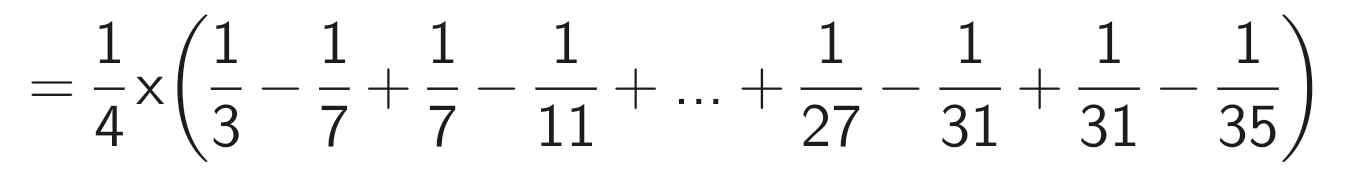
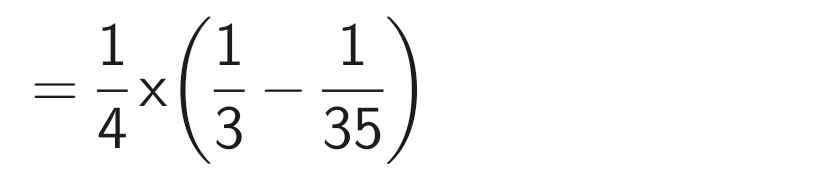


\(A=2.5+5.8+8.11+...+293.296+296.299\\ 9A=2.5.9+5.8.9+8.11.9+...+293.296.9+296.299.9\\ 9A=2.5.9+5.8.\left(11-2\right)+8.11.\left(14-5\right)+...+293.296.\left(299-290\right)+296.299.\left(302-293\right)\)\(9A=2.5.9+5.8.11-2.5.8+8.11.14-5.8.11+...+293.296.299-290.293.296+296.299.302-293.296.299\)\(9A=2.5.9-2.5.8+296.299.302\\9A=10+296.299.302 \\ A=\dfrac{10+296.299.302}{9}=2969802\)