x^2-9x+8=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 2(a+b)-a+3b
=2a+2b-a+3b
=a+5b
b: 4(3a-4b)+5(2a+b)
=12a-16b+10a+5b
=12a+10a-16b+5b
=22a-11b

a: ta có; AM+MB=AB
BN+NC=BC
CP+PD=CD
DQ+QA=DA
mà AB=BC=CD=DA và AM=BN=CP=DQ
nên MB=NC=PD=QA
Xét ΔQAM vuông tại A và ΔNCP vuông tại C có
QA=NC
AM=CP
Do đó: ΔQAM=ΔNCP
b: ΔQAM=ΔNCP
=>QM=PN
Xét ΔMBN vuông tại B và ΔPDQ vuông tại D có
MB=PD
BN=DQ
Do đó: ΔMBN=ΔPDQ
=>MN=PQ
Xét ΔMAQ vuông tại A và ΔNBM vuông tại B có
MA=NB
AQ=BM
Do đó: ΔMAQ=ΔNBM
=>MQ=MN
Ta có: ΔMAQ=ΔNBM
=>\(\widehat{AMQ}=\widehat{BNM}\)
=>\(\widehat{AMQ}+\widehat{BMN}=90^0\)
Ta có: \(\widehat{AMQ}+\widehat{QMN}+\widehat{NMB}=180^0\)
=>\(\widehat{QMN}+90^0=180^0\)
=>\(\widehat{QMN}=90^0\)
Xét tứ giác MNPQ có
MN=PQ
MQ=PN
Do đó: MNPQ là hình bình hành
Hình bình hành MNPQ có MN=MQ
nên MNPQ là hình thoi
Hình thoi MNPQ có \(\widehat{QMN}=90^0\)
nên MNPQ là hình vuông

a) \(...\Rightarrow x\left(x^2-16\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-16=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm4\end{matrix}\right.\)
b) \(...\Rightarrow x\left(x^3-2x^2+10x-20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^3-2x^2+10x-20=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left(x-2\right)\left(x^2+10\right)=0\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x^2+10=0\left(vô.lý\right)\end{matrix}\right.\Leftrightarrow x=2\)
Vậy \(x\in\left\{0;2\right\}\)
c) \(...\Rightarrow\left[{}\begin{matrix}2x-3=x+5\\2x-3=-x-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\3x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-\dfrac{2}{3}\end{matrix}\right.\)
d) \(...\Rightarrow x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x^2-4x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
a; \(x^3\) - 16\(x\) = 0
\(x\)(\(x^2\) - 16) = 0
\(\left[{}\begin{matrix}x=0\\x^2=16\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x^2=\left(-4\right)^2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-4\\x=4\end{matrix}\right.\)
Vậy \(x\) \(\in\) {0; -4; 4}

\(x^2\) - 7\(x\) - 8
= (\(x^2\) + \(x\)) - 8\(x\) - 8
= \(x\).(\(x\) + 1) - 8.(\(x\) + 1)
= (\(x+1\)).(\(x-8\))

2:
a: DB=DC
=>D là trung điểm của BC
DM=DN
mà D nằm giữa M và N
nên D là trung điểm của MN
Xét tứ giác BMCN có
D là trung điểm chung của BC và MN
=>BMCN là hình bình hành
b: Ta có: BMCN là hình bình hành
=>BM//CN
mà BM\(\perp\)AC
nên CN\(\perp\)AC
Xét tứ giác BKCN có
BK//CN
BK\(\perp\)KC
Do đó: BKCN là hình thang vuông
c: Để BMCN là hình thoi thì MN\(\perp\)BC
hay MD\(\perp\)BC
Xét ΔABC có
BK,CH là các đường cao
BK cắt CH tại M
Do đó: M là trực tâm của ΔABC
=>AM\(\perp\)BC
ta có: AM\(\perp\)BC
MD\(\perp\)BC
mà AM,MD có điểm chung là M
nên A,M,D thẳng hàng
Xét ΔABC có
AD là đường cao
AD là đường trung tuyến
Do đó: ΔABC cân tại A
=>AB=AC
1: Diện tích đáy là; \(4000\cdot3:30=4000:10=400\left(cm^2\right)\)
Độ dài cạnh đáy là \(\sqrt{400}=20\left(cm\right)\)

Gọi đường thẳng cần tìm là (d): y=ax+b(a<>0)
Thay x=-3 và y=0 vào (d), ta được:
\(a\cdot\left(-3\right)+b=0\)
=>-3a+b=0
=>b=3a
=>(d): y=ax+3a
Thay x=0 và y=2 vào (d), ta được:
\(a\cdot0+3a=2\)
=>3a=2
=>\(a=\dfrac{2}{3}\)
Vậy: (d): \(y=\dfrac{2}{3}x+3\cdot\dfrac{2}{3}=\dfrac{2}{3}x+2\)

Bài 4:
a: Xét tứ giác ADME có \(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
nên ADME là hình chữ nhật
b: Ta có: MD\(\perp\)AB
AC\(\perp\)AB
Do đó: MD//AC
Ta có: ME\(\perp\)AC
AB\(\perp\)AC
Do đó: ME//AB
Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó:D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Ta có: EM=AD(ADME là hình chữ nhật)
AD=DB
Do đó; EM=BD
Xét tứ giác BDEM có
BD//EM
BD=EM
Do đó: BDEM là hình bình hành
c: ADME là hình chữ nhật
=>AM=DE
Ta có: ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
=>O là trung điểm chung của AM và DE
Ta có: \(OA=OM=\dfrac{AM}{2}\)
\(OD=OE=\dfrac{DE}{2}\)
mà AM=DE
nên OA=OM=OD=OE=AM/2=DE/2
ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}\)
=>\(2OE=\dfrac{BC}{2}\)
=>BC=4OE
d: Ta có: ΔHAC vuông tại H
mà HE là đường trung tuyến
nên HE=AE
mà AE=MD(ADME là hình chữ nhật)
nên HE=MD
Ta có: BDEM là hình bình hành
=>DE//MB
=>DE//BC
=>DE//HM
Xét tứ giác HMED có
HM//ED
HE=MD
Do đó: HMED là hình thang cân
e: Xét tứ giác ABCI có
E là trung điểm chung của AC và BI
=>ABCI là hình bình hành
=>AI//BC
Xét tứ giác AMCF có
E là trung điểm chung của AC và MF
=>AMCF là hình bình hành
=>AF//CM
=>AF//BC
ta có: AF//BC
AI//BC
mà AF,AI có điểm chung là A
nên A,F,I thẳng hàng
Bài 6:
\(B=x^4-4x^3-2x^2+12x+9\)
\(=x^4-3x^3-x^3+3x^2-5x^2+15x-3x+9\)
\(=x^3\left(x-3\right)-x^2\left(x-3\right)-5x\left(x-3\right)-3\left(x-3\right)\)
\(=\left(x-3\right)\left(x^3-x^2-5x-3\right)\)
\(=\left(x-3\right)\left(x^3-3x^2+2x^2-6x+x-3\right)\)
\(=\left(x-3\right)\left(x-3\right)\cdot\left(x^2+2x+1\right)\)
\(=\left(x-3\right)^2\cdot\left(x+1\right)^2=\left[\left(x-3\right)\left(x+1\right)\right]^2\)
=>B là bình phương của một số nguyên

a) Sau a phút, lượng nước có trong bể là:
\(x-y\left(l\right)\)
b) Sau b phút, vòi nước chảy vào được số lít nước là: \(bx\left(l\right)\)
Lượng nước trong bể:
\(5+x-y+bx\left(l\right)\)

\(A=\left(x^3+3x^2y+3xy^2+y^3\right)-3\left(x^2+2xy+y^2\right)+3\left(x+y\right)+2020\)
\(=\left(x+y\right)^3-3\left(x+y\right)^2+3\left(x+y\right)-1+2021\)
\(=\left(x+y-1\right)^3+2021\)
\(=4040^3+2021\)

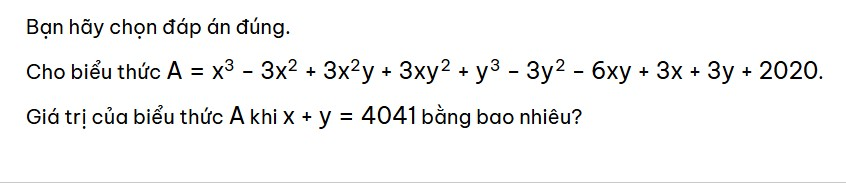
\(x^2-9x+8=0\)
=>\(x^2-x-8x+8=0\)
=>x(x-1)-8(x-1)=0
=>(x-1)(x-8)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=8\end{matrix}\right.\)
x^2-9x+8=0
(x-8)(x-1)=0
x=8 hoặc x=1.