\(\left(a^6-b^3\right)=\left(a^2-b\right)\left(a^4+a^2b+b^2\right)\)

\(=\left(a^2-b\right)\left(a^4+a^2b+b^2\right)\)

\(a.x^2-7x-3x+21=0\Leftrightarrow\left(x^2-7x\right)-\left(3x-21\right)=0\)

\(\Leftrightarrow x\left(x-7\right)-3\left(x-7\right)=0\Leftrightarrow\left(x-3\right)\left(x-7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=7\end{matrix}\right.\)

\(b.x^2+6x+2x+12=0\Leftrightarrow\left(x^2+6x\right)+\left(2x+12\right)=0\)

\(\Leftrightarrow x\left(x+6\right)+2\left(x+6\right)=0\Leftrightarrow\left(x+2\right)\left(x+6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-6\end{matrix}\right.\)

\(c.x^2+4x+5x+20=0\Leftrightarrow\left(x^2+4x\right)+\left(5x+20\right)=0\)

\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\Leftrightarrow\left(x+5\right)\left(x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-4\end{matrix}\right.\)

\(Ax=Bx\Rightarrow Ax-Bx=0\Rightarrow x\left(A-B\right)=0\Rightarrow x=0\) \(\rightarrow câu.A\)

A.(0)
B.(1)
C(0,1,5)
D.(0,1,5,6)
chọn đáp án thôi là đc ak

Lời giải:

a. $x^2-y^2+8x-8y=(x^2-y^2)+(8x-8y)$

$=(x-y)(x+y)+8(x-y)=(x-y)(x+y+8)$

b. $4x^2+4xy+y^2-4x-2y=(4x^2+4xy+y^2)-(4x+2y)$

$=(2x+y)^2-2(2x+y)=(2x+y)(2x+y-2)$

c.

$x^3+y^3+4x+4y=(x^3+y^3)+(4x+4y)$

$=(x+y)(x^2-xy+y^2)+4(x+y)$

$=(x+y)(x^2-xy+y^2+4)$

d.

$=(x^3-3x^2y+3xy^2-y^3)+(x^2-y^2)=(x-y)^3+(x-y)(x+y)$

$=(x-y)[(x-y)^2+(x+y)]=(x-y)(x^2-2xy+y^2+x+y)$

e.

$x^2+3x+2=(x^2+x)+(2x+2)=x(x+1)+2(x+1)$

$=(x+1)(x+2)$

f.

$x^2-7x+6=(x^2-6x)-(x-6)=x(x-6)-(x-6)=(x-1)(x-6)$

h.

Đa thức không phân tích được thành nhân tử với hệ số nguyên.

bằng 2

2 nhé

​

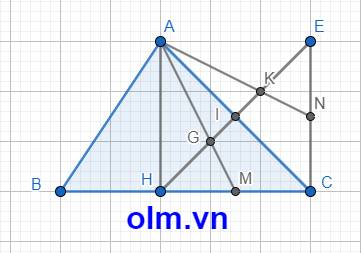
a, Xét tứ AHCE ta có: IH = IE ; IA = IC 

⇒ tứ giácAHCE là hình bình hành (1)

Mà AH \(\perp\)  BC \(\equiv\)  H nên ⇒ \(\widehat{AHC}\) = 90⁰ (2)

Kết hợp (1) và (2) ta có: Tứ giác AHCE là hình chữ nhật (đpcm).

b, Xét tam giác AHC có: M là trung  điểm HC; I là trung điểm AC

⇒ AM; HI lần lượt là trung tuyến của tam  giác AHC

⇒ G là trọng tâm của tam giác AHC ⇒ HG = \(\dfrac{2}{3}\)HI ⁽³⁾

IG = HI - HG = HI - \(\dfrac{2}{3}\)HI = \(\dfrac{1}{3}\)HI 

Chứng minh tương tự ta có: KE = \(\dfrac{2}{3}\)IE = \(\dfrac{2}{3}\)HI ⁽⁴⁾ ( vì IE = HI)

IK = IE - KE =  IE - \(\dfrac{2}{3}\)IE = \(\dfrac{1}{3}\)IE = \(\dfrac{1}{3}\)HI (vì HI = IE)

GK = IG + IK = \(\dfrac{1}{3}\)HI + \(\dfrac{1}{3}\)HI = \(\dfrac{2}{3}\)HI ⁽⁵⁾  

Kết hợp(3); (4); (5) ta có: HG = GK = KE (đpcm)

chưa vẽ được

tick cho mình cái 

Bài tập 1

a) Chứng minh AFOE cân

Xét tam giác AOB và tam giác FOE, ta có:

• AB = FO (do B là đỉnh chéo của hình bình hành ABCD)
• AO = OF (do O là giao điểm của các đường chéo)
• AE = OF (do F nằm trên cạnh BC)

Do đó, hai tam giác AOB và FOE đồng dạng theo tỉ số 1:1.

Vậy, AFOE cân tại F.

b) Trên tia đối của tòa FB lấy điểm 1 sao cho F1 = FB. Chứng minh OF = h OE == DI

Xét tam giác F1OB và tam giác FOE, ta có:

• FB = F1B (do F1 = FB)
• FO = OF (do O là giao điểm của các đường chéo)
• BE = FE (do F nằm trên cạnh BC)

Do đó, hai tam giác F1OB và FOE đồng dạng theo tỉ số 1:1.

Vậy, OF = OE = DI.

c) Gia sư BAD =50. Tính EOF

Xét tam giác EOF, ta có:

• EO = OE (do O là giao điểm của các đường chéo)
• OF = OE = DI = 50/2 = 25

Do đó, EOF = 25^2 = 625.

Kết luận

• AFOE cân tại F
• OF = OE = DI = 25
• EOF = 625

Bài tập 2

Chứng minh 1 đổi xứng với K qua Đ

Xét tam giác AFE và tam giác BKF, ta có:

• AE = CF (do cho AE = CF)
• AF = BF (do do A và B là các đỉnh chéo của hình bình hành ABCD)
• EF = FB (do F nằm trên cạnh BC)

Do đó, hai tam giác AFE và BKF đồng dạng theo tỉ số 1:1.

Vậy, I đối xứng với K qua D.

Kết luận

I đối xứng với K qua D.

Bài tập 3

Chứng minh Nạp là hai điểm đối xứng nhau qua ở

Xét tam giác MNO và tam giác MNP, ta có:

• MN = MN (đồng nhất)
• NO = NP (do N và P lần lượt đối xứng với M qua a và b)
• MO = MP (do O là giao điểm của các đường chéo a và b)

Do đó, hai tam giác MNO và MNP đồng dạng theo tỉ số 1:1.

Vậy, N và P là hai điểm đối xứng nhau qua O.

Kết luận

N và P là hai điểm đối xứng nhau qua O.

Chúc bạn học tốt!

a²+b²+c²=(a²+2ac+c²)-2ac+b²=(a+c)²-2b²+b²=(a+b+c)(a-b+c)
mà a²+b²+c² là số nguyên tố và a+b+c>a-b+c nên a-b+c=1
=> a+c=b+1 => a²+2ac+c²=b²+2b+1 => a²+b²=2b+1=2a+2c+1+1
=>a²-2a+1+c²-2c+1=0 => (a-1)²+(c-1)²=0=>a=c=1=>b=1
Vậy (a,b,c) cần tìm là (1,1,1)