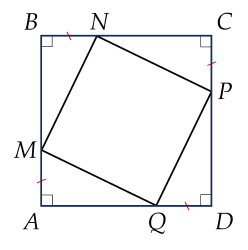
Cho hình vuông $ABCD$. Trên các cạnh $AB, \, BC,$ $CD, \, DA$ lấy lần lượt các điểm $M, \, N, \, P, \, Q$ sao cho $AM=BN=CP=DQ.$
a) Chứng minh $MB=NC=PD=QA.$
b) Chứng minh $\Delta QAM=\Delta NCP.$
c) Chứng minh $MNPQ$ là hình vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hbh ABCD có AB =CD;AB//CD
+) lần lượt là trung điểm của
lần lượt là nằm trên của .
=> AM//CN
a) là hình bình hành nên suy ra
Do đó .
Tứ giác có // nên là hình bình hành.
Lại có vuông tại có là đường trung tuyến nên .
Hình bình hành có hai cạnh kề bằng nhau nên là hình thoi, khi đó hai đường chéo vuông góc với nhau.
Tứ giác là hình thoi.

a/
Ta có
IA=IC (gt); IM=IK (gt) => AMCK là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Ta có
MB=MC (gt); IA=IC (gt) => MI là đường trung bình của tg ABC => MI//AB
Mà \(AB\perp AC\)
\(\Rightarrow MI\perp AC\Rightarrow MK\perp AC\)
=> AMCK là hình thoi (Hình bình hành có 2 đường chéo vuông góc là hình thoi)
b/
Ta có
MI//AB (cmt) => MK//AB
AK//MC (cạnh đối hbh AMCK) => AK//MB
=> AKMB là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
c/
Để AMCK là hình vuông \(\Rightarrow AM\perp BC\) => AM là đường cao của tg ABC
Mà AM là trung tuyến của tg ABC (gt)
=> ABC cân tại A (Tam giác có đường cao đồng thời là đường trung tuyến là tg cân)
=> Để AMCK là hình vuông thì tg ABC vuông cân tại A
a) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
vuông tại có là đường trung tuyến nên .
Vậy hình bình hành có nên là hình thoi.
b) Vì là hình thoi nên // và .
Tứ giác có // nên là hình bình hành.
c) Để là hình vuông thì cần có một góc vuông hay .
Khi đó có vừa là đường cao vừa là đường trung tuyến nên cân tại .
Vậy vuông cân tại thì là hình vuông.

a) vuông cân nên góc B= góc C = 45 độ
Tam giácBHE vuông tại H có góc BEH + góc B = 90 độ
Suy ra góc BEH = 90 độ - 45 độ = 45 độ nên góc B= góc BEH = 45 độ
Vậy tam giác BEH vuông tại H
b) Chứng minh tương tự như câu a ta được tam giác CFG vuông tại G nên GF=GC và HB=HE
Lại có BH=HG=GC suy ra EH=HG=GF và EH//FG ( cùng vuông góc với BC)
Tứ giác EFGH có EH//FG, EH=FG
=>tứ giác EFGH là hình bình hành
Xét hình bình hành có một góc vuông là góc H nên là hình chữ nhật
Mà hình chữ nhật có hai cạnh kề bằng nhau là EH=HG nên là hình vuông
Vậy EFGH là hình vuông
a) vuông cân nên
vuông tại có
Suy ra nên .
Vậy vuông cân tại
b) Chứng minh tương tự câu a ta được vuông cân tại nên và
Mặt khác suy ra và // (cùng vuông góc với
Tứ giác có // nên là hình bình hành.
Hình bình hành có một góc vuông nên là hình chữ nhật
Hình chữ nhật có hai cạnh kề bằng nhau nên là hình vuông.

\(AC\perp Oy\) (gt); \(Ox\perp Oy\) (gt) => AC//Oy => AC//OB
C/m tương tự có AB//OC
=> OBAC là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{xOy}=90^o\)
=> OBAC là HCN
Ta có
AC=AB (Tính chất đường phân giác)
=> OBAC là hình vuông
Tứ giác có ba góc vuông: góc B= góc C = góc BOC= 90 độ
Nên là hình chữ nhật.
Mà nằm trên tia phân giác suy ra .
Khi đó là hình vuông.

Ta có:
|x - 1| + |x - 7|
= |x - 1| + |7 - x|
≥ |x - 1 + 7 - x| = 6
Vậy |x + 1| + |x - 7| ≥ 6

`B=y^2-4y+5`
`=y^2-4y+4+1`
`=(y-2)^2+1`
với `y=12` ta có
`(12-2)^2+1=10^2+1=100+1=101`
Với y=12, ta có
12² - 4x12 + 5
= 144 - 48 + 5
= 96 + 5=101

Góc DAC là góc nằm trong tam giác ABD, nên ta có thể tính được bằng cách lấy tổng các góc trong tam giác ABD trừ đi góc ADB: Góc DAC = 180° - góc ABD = 180° - 60° = 120°
Góc ADB là góc nằm trong tam giác CBD, nên ta có thể tính được bằng cách lấy tổng các góc trong tam giác CBD trừ đi góc CDB:
Góc ADB = 180° - góc CBD = 180° - 20° = 160°
Vậy số đo các góc DAC và ADB lần lượt là 120° và 160°.

Nếu m hoặc n chia hết cho 3 thì hiển nhiên \(nm\left(m^2-n^2\right)⋮3\)
Nếu cả m và n đều không chia hết cho 3 thì \(m^2,n^2\) đều chia 3 dư 1 (tính chất của số chính phương). Do đó \(m^2-n^2⋮3\) nên \(mn\left(m^2-n^2\right)⋮3\)
Vậy \(mn\left(m^2-n^2\right)⋮3\) với mọi cặp số nguyên m, n.
a) Do ABCD là hình vuôn nên:
\(AB=BC=CD=AD\)
Mà: \(\left\{{}\begin{matrix}AB=AM+MB\\BC=BN+NC\\CD=CP+PD\\AD=DQ+QA\end{matrix}\right.\)
Lại có: \(AM=BN=CP=DQ\)
\(\Rightarrow MB=NC=PD=QA\left(dpcm\right)\)
b) Xét \(\Delta QAM\) và \(\Delta NCP\) có:
\(\widehat{A}=\widehat{C}=90^o\left(gt\right)\)
\(AM=CP\left(gt\right)\)
\(QA=NC\left(cmt\right)\)
\(\Rightarrow\Delta QAM=\Delta NCP\left(c.g.c\right)\)
c) Xét các tam giác: \(\Delta QAM,\Delta NCP,\Delta PDQ,\Delta MBN\) ta có:
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^o\left(gt\right)\)
\(AM=BN=CP=DQ\left(gt\right)\)
\(MB=NC=PD=QA\left(cmt\right)\)
\(\Rightarrow\Delta QAM=\Delta NCP=\Delta PDQ=\Delta MBN\left(c.g.c\right)\)
\(\Rightarrow MQ=QP=PN=NM\) (các cạnh tương ứng)
\(\Rightarrow MNPQ\) là hình thoi (1)
Xét tam giác QAM ta có:
\(\widehat{QMA}+\widehat{AQM}=180^o-90^o=90^o\)
Mà: \(\Delta QAM=\Delta MBN\left(cmt\right)\)
\(\Rightarrow\widehat{BMN}=\widehat{AQM}\) (hai góc tương ứng)
\(\Rightarrow\widehat{BMN}+\widehat{QMA}=90^o\)
Lại có: \(\widehat{BMN}+\widehat{QMA}+\widehat{NMQ}=180^o\)
\(\Rightarrow\widehat{NMQ}=180^o-90^o=90^o\) (2)
Từ (1) và (2) ta có MNPQ là hình vuông
a) ����ABCD là hình vuông nên ��=��=��=��AB=BC=CD=DA
Mà ��=��=��=��AM=BN=CP=DQ.
Trừ theo vế ta được ��−��=��−��=��−��=��−��AB−AM=BC−BN=CD−CP=DA−DQ
Suy ra ��=��=��=��MB=NC=PD=QA
Xét tam giác QAM và tam giác NPC có:
góc A = góc C = 90 độ
AQ=NC(cmt)
AM=CP(gt)
=>Tam giác QAM= tam giác NPC(c.g.c)
c)=> NP = MQ ( hai cạnh tương ứng)
Chứng minh tương tự như phần b ta có: Tam giác QAM= tam giác PDQ và tam giác QAM= tam giác MBN
Khi đó: MQ=PQ, MN=MQ và góc AMQ= góc DQP
Mà góc AMQ+AQM=90 độ
=>góc DQP+ góc AQM= 90 độ
Do đó góc MQP = 90 độ
tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi
Lại có góc MQP = 90 độ nên là hình vuông
Vậy tứ giác MNPQ là hình vuông