Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

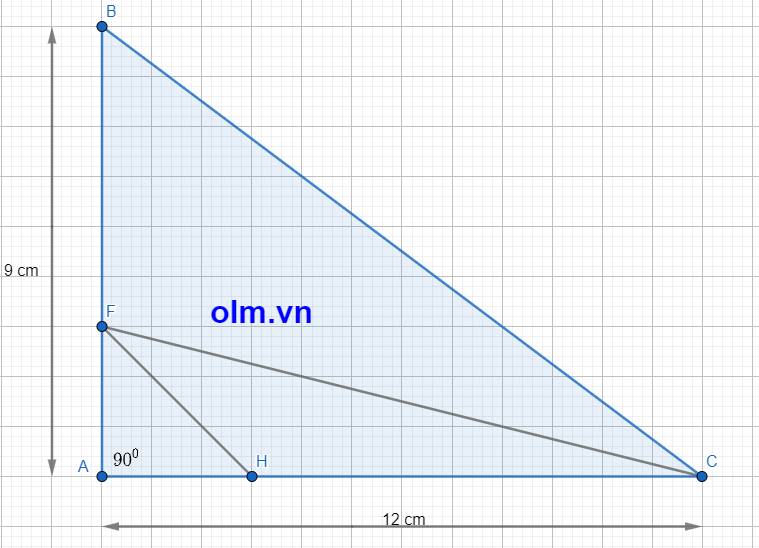
a, Diện tích của tam giác ABC là: 9\(\times\)12: 2= 54 (cm2)
b, HC = AC - AH = AC - \(\dfrac{1}{4}\)AC= \(\dfrac{3}{4}\)AC
SFHC = \(\dfrac{3}{4}\)SACF (vì hai tam giác có chung chiều cao hạ từ đỉnh F xuống đáy AC và HC = \(\dfrac{3}{4}\)AC)
Độ dài AF bằng: \(\dfrac{1}{3-1}\)BF = \(\dfrac{1}{2}\)BF
SACF = \(\dfrac{1}{2}\) SFBC ( vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AF và AF = \(\dfrac{1}{2}\)BF)
Tỉ số diện tích của tam giác FHC và diện tich tam giác FBC là:
\(\dfrac{3}{4}\) \(\times\) \(\dfrac{1}{2}\) = \(\dfrac{3}{8}\)
Đáp số: a, 54 cm2
b, \(\dfrac{3}{8}\)

Lần sau chú ý đăng đúng môn học nha.
\(a,3^4.3^5.3^6=3^{\left(4+5+6\right)}=3^{15}\)
\(b,5^2.5^4.5^5.25=5^2.5^4.5^5.5^2=5^{\left(2+4+5+2\right)}=5^{13}\)
\(c,10^8:10^3=10^8.\dfrac{1}{10^3}=10^5\)
\(d,a^7:a^2=a^7.\dfrac{1}{a^2}=\dfrac{a^7}{a^2}=a^5\)

S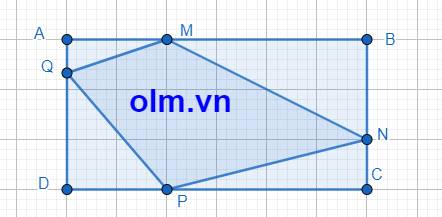
AQ = DA - DQ = DA - \(\dfrac{3}{4}\)DA = \(\dfrac{1}{4}\)DA
SAMQ = \(\dfrac{1}{4}\)SAMD (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy AD và AQ = \(\dfrac{1}{4}\)AD)
SAMD = \(\dfrac{1}{3}\)SABD ( vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AB và AM = \(\dfrac{1}{3}\)AB)
SABD = \(\dfrac{1}{2}\)SABCD(vì ABCD là hình chữ nhật)
SAMQ = \(\dfrac{1}{4}\times\dfrac{1}{3}\times\dfrac{1}{2}\)SABCD = 216\(\times\) \(\dfrac{1}{24}\) = 9 (cm2)
SMBN = \(\dfrac{2}{3}\)SBCM (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{2}{3}\)BC)
BM = AB - AM = AB - \(\dfrac{1}{3}\)AB = \(\dfrac{2}{3}\)AB
SBCM = \(\dfrac{2}{3}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM = \(\dfrac{2}{3}\)AB)
SABC = \(\dfrac{1}{2}\)SABCD (vì ABCD là hình chữ nhật)
SMBN = \(\dfrac{2}{3}\times\dfrac{2}{3}\times\dfrac{1}{2}\)SABCD = 216\(\times\)\(\dfrac{2}{9}\) = 48 (cm2)
CN = BC - BN = BC - \(\dfrac{2}{3}\)BC = \(\dfrac{1}{3}\)BC
SCPN = \(\dfrac{1}{3}\)SPBC (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{1}{3}\)BC)
SPBC = \(\dfrac{2}{3}\)SBCD (vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy CD và CP = \(\dfrac{2}{3}\)CD)
SBCD = \(\dfrac{1}{2}\)SABCD (vì ABCD là hình chữ nhật)
SCPN = \(\dfrac{1}{3}\times\dfrac{2}{3}\times\dfrac{1}{2}\)SABCD = 216 \(\times\) \(\dfrac{1}{9}\) = 24 (cm2)
SDPQ = \(\dfrac{3}{4}\)SDPA (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy DA và DQ = \(\dfrac{3}{4}\)DA)
DP = CP - DC = DC - \(\dfrac{2}{3}\)DC = \(\dfrac{1}{3}\)DC
SDPA = \(\dfrac{1}{3}\)SACD(vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy CD và DP = \(\dfrac{1}{3}\)DC)
SACD = \(\dfrac{1}{2}\)SABCD(vì ABCD là hình chữ nhật)
SDPQ = \(\dfrac{3}{4}\times\dfrac{1}{3}\times\dfrac{1}{2}\) SABCD = 216 \(\times\) \(\dfrac{1}{8}\) = 27 (cm2)
SMNPQ = 216 - (9+ 48 + 24 + 27) = 108(cm2)
Đáp số: 108 cm2

\(\dfrac{4}{9}-x=\dfrac{1}{8}\\ x=\dfrac{4}{9}-\dfrac{1}{8}=\dfrac{32}{72}-\dfrac{9}{72}\\ x=\dfrac{23}{72}\)
\(\dfrac{4}{9}-x=\dfrac{1}{8}\)
`\Rightarrow`\(x=\dfrac{4}{9}-\dfrac{1}{8}\)
`\Rightarrow`\(x=\dfrac{23}{72}\)

Trước hết ta cần xem xét điều sau: Nếu 2 tam giác có chung đường cao thì tỉ số diện tích giữa 2 tam giác đó bằng tỉ số độ dài 2 cạnh đáy tương ứng.
Điều này khá dễ thấy vì giả sử có hình vẽ trên thì \(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{\dfrac{1}{2}\times AH\times BD}{\dfrac{1}{2}\times AH\times CD}=\dfrac{BD}{CD}\)
Tiếp đến, ta có tiếp điều sau: Cho tam giác ABC bất kì. Các điểm E, F lần lượt nằm trên các cạnh AC, AB. Khi đó \(\dfrac{S_{AEF}}{S_{ABC}}=\dfrac{AE\times AF}{AB\times AC}\) (tạm gọi đây là (*))
Điều này trở nên dễ thấy nhờ điều ta mới đề cập đến ở trên. Vì \(\dfrac{S_{AEF}}{S_{ABE}}=\dfrac{AF}{AB}\) và \(\dfrac{S_{ABE}}{S_{ABC}}=\dfrac{AE}{AC}\) nên nhân vế theo vế rồi rút gọn, ta được: \(\dfrac{S_{AEF}}{S_{ABC}}=\dfrac{AE\times AF}{AB\times AC}\).
Bây giờ, ta quay lại bài toán chính.
Áp dụng (*) cho tam giác ABD với 2 điểm M, Q nằm trên AB, AD, ta được \(\dfrac{S_{AMQ}}{S_{ABD}}=\dfrac{AM}{AB}\times\dfrac{AQ}{AD}=\dfrac{2}{3}\times\dfrac{2}{3}=\dfrac{4}{9}\) (1)
Tương tự, ta cũng có \(\dfrac{S_{BMN}}{S_{BAC}}=\dfrac{BM}{BA}\times\dfrac{BN}{BC}=\dfrac{1}{3}\times\dfrac{2}{3}=\dfrac{2}{9}\) (2)
\(\dfrac{S_{CNP}}{S_{CBD}}=\dfrac{CN}{CB}\times\dfrac{CP}{CD}=\dfrac{1}{3}\times\dfrac{1}{2}=\dfrac{1}{6}\) (3)
\(\dfrac{S_{DPQ}}{S_{DCA}}=\dfrac{DP}{DC}\times\dfrac{DQ}{DA}=\dfrac{1}{2}\times\dfrac{1}{3}=\dfrac{1}{6}\) (4)
Hơn nữa, nhận thấy rằng diện tích của 4 tam giác ABD, BAC, CBD và DCA đều bằng nhau và bằng \(\dfrac{1}{2}\) diện tích của hình chữ nhật ABCD nên cộng theo vế (1), (2), (3) và (4) suy ra:
\(\dfrac{S_{AQM}+S_{BMN}+S_{CNP}+S_{DPQ}}{\dfrac{1}{2}S_{ABCD}}=1\), mà tổng diện tích của 4 tam giác AQM, BMN, CNP và DPQ chính bằng \(S_{ABCD}-S_{MNPQ}\) nên ta có \(\dfrac{S_{ABCD}-S_{MNPQ}}{\dfrac{1}{2}S_{ABCD}}=1\) \(\Leftrightarrow S_{ABCD}-S_{MNPQ}=\dfrac{1}{2}S_{ABCD}\) \(\Leftrightarrow S_{MNPQ}=\dfrac{1}{2}S_{ABCD}=\dfrac{1}{2}.496=216\left(cm^2\right)\)
Vậy \(S_{MNPQ}=216cm^2\)

SMNPQ = \(\dfrac{1}{2}\) x SABCD = 288 (cm2)
HD: Hình chữ nhật chia thành 4 hình tam giác vuông và hình thoi MNPQ

\(S_{AMQ}=\dfrac{1}{2}\cdot AM\cdot AQ=\dfrac{1}{2}\cdot\dfrac{1}{2}AB\cdot\dfrac{1}{2}AD=144\cdot\dfrac{1}{8}=18\left(cm^2\right)\)
\(S_{MBN}=\dfrac{1}{2}\cdot MB\cdot BN=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot AB\cdot\dfrac{1}{3}BC=\dfrac{1}{12}\cdot144=12\left(cm^2\right)\)
\(S_{NCP}=\dfrac{1}{2}\cdot NC\cdot CP=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot BC\cdot\dfrac{2}{3}\cdot CD=\dfrac{2}{9}\cdot144=32\left(cm^2\right)\)
\(S_{QDP}=\dfrac{1}{2}\cdot QD\cdot DP=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot AD\cdot\dfrac{1}{3}CD=\dfrac{1}{12}\cdot144=12\left(cm^2\right)\)
\(\Rightarrow S_{MNPQ}=144-18-12-32-12=70\left(cm^2\right)\)
Hướng dẫn:
SMNPQ = SABCD - (SAMQ+SBMN+SCNP+SPDQ)
+ Tính diện tích 4 tam giác theo độ dài của chiều dài và chiều rộng hình chữ nhật
+ Từ đó tính được:
SMNPQ =73 (cm2)

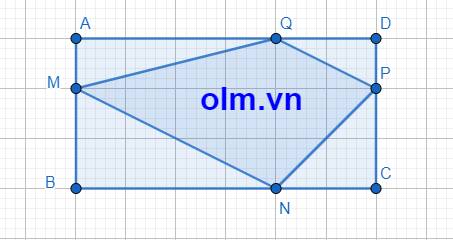
SAMQ = \(\dfrac{1}{3}\)SABQ (vì hai tam giác có chung chiều cao hạ từ đỉnh Q xuống đáy AB và AM = \(\dfrac{1}{3}\)ABQ)
AQ = DA - QD = DA - \(\dfrac{1}{3}\)DA = \(\dfrac{2}{3}\)DA
SABQ = \(\dfrac{2}{3}\)SABD (vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AD và QA = \(\dfrac{2}{3}\)DA)
SABD = \(\dfrac{1}{2}\) SABCD (vì ABCD là hình chữ nhật)
SAMQ = \(\dfrac{1}{3}\)\(\times\)\(\dfrac{2}{3}\)\(\times\)\(\dfrac{1}{2}\) \(\times\) SABCD = 162 \(\times\) \(\dfrac{1}{9}\) = 18 (cm2)
SBMN = \(\dfrac{2}{3}\)SBCM (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{2}{3}\)BC)
BM = AB - AM = AB - \(\dfrac{1}{3}\)AB = \(\dfrac{2}{3}\)AB
SBCM = \(\dfrac{2}{3}\)SABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM = \(\dfrac{2}{3}\)AB)
SABC = \(\dfrac{1}{2}\)SABCD ( vì ABCD là hình chữ nhật)
SBMN = \(\dfrac{2}{3}\times\dfrac{2}{3}\) \(\times\) \(\dfrac{1}{2}\)SABCD = 162 \(\times\) \(\dfrac{2}{9}\) = 36 (cm2)
CN = BC - BN = BC - \(\dfrac{2}{3}\)BC = \(\dfrac{1}{3}\)BC
SPCN = \(\dfrac{1}{3}\)SBPC( vì hai tam giác có cùng chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{1}{3}\)BC
SPBC = \(\dfrac{2}{3}\)SBCD (vì hai tam giác có cùng chiều cao hạ từ đỉnh B xuống đáy CD và CP = \(\dfrac{2}{3}\)CD)
SBCD = \(\dfrac{1}{2}\)SABCD ( vì ABCD là hình chữ nhật)
SPCN = \(\dfrac{1}{3}\times\dfrac{2}{3}\times\dfrac{1}{2}\)SABCD = 162\(\times\)\(\dfrac{1}{9}\) = 18(cm2)
DP = DC - CP = DC - \(\dfrac{2}{3}\)DC = \(\dfrac{1}{3}\)DC
SDPQ = \(\dfrac{1}{3}\)SDCQ (vì hai tam giác có chung chiều cao hạ từ đỉnh Q xuống đáy DC và DP = \(\dfrac{1}{3}\)DC)
SDCQ = \(\dfrac{1}{3}\)SACD (vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AD và DQ = \(\dfrac{1}{3}\)AD)
SADC = \(\dfrac{1}{2}\)SABCD ( vì ABCD là hình chữ nhật)
SDPQ = \(\dfrac{1}{3}\times\dfrac{1}{3}\times\dfrac{1}{2}\)SABCD = 162 \(\times\) \(\dfrac{1}{18}\) = 9 (cm2)
SMNPQ = SABCD - (SDPQ + SPCN + SBMN + SAQM)
SMNPQ = 162 - (9 + 18 + 36 + 18) = 81 (cm2)
Đáp số : 81 cm2
Số viên bi Bình có là:
\(viên bi)
Tổng số viên bi của Bình và An là:
(viên bi)
Trung bình cộng số viên bi của 3 bạn là:
(viên bi)
Số viên bi của Thịnh là:
(viên bi)
Đáp số: ...

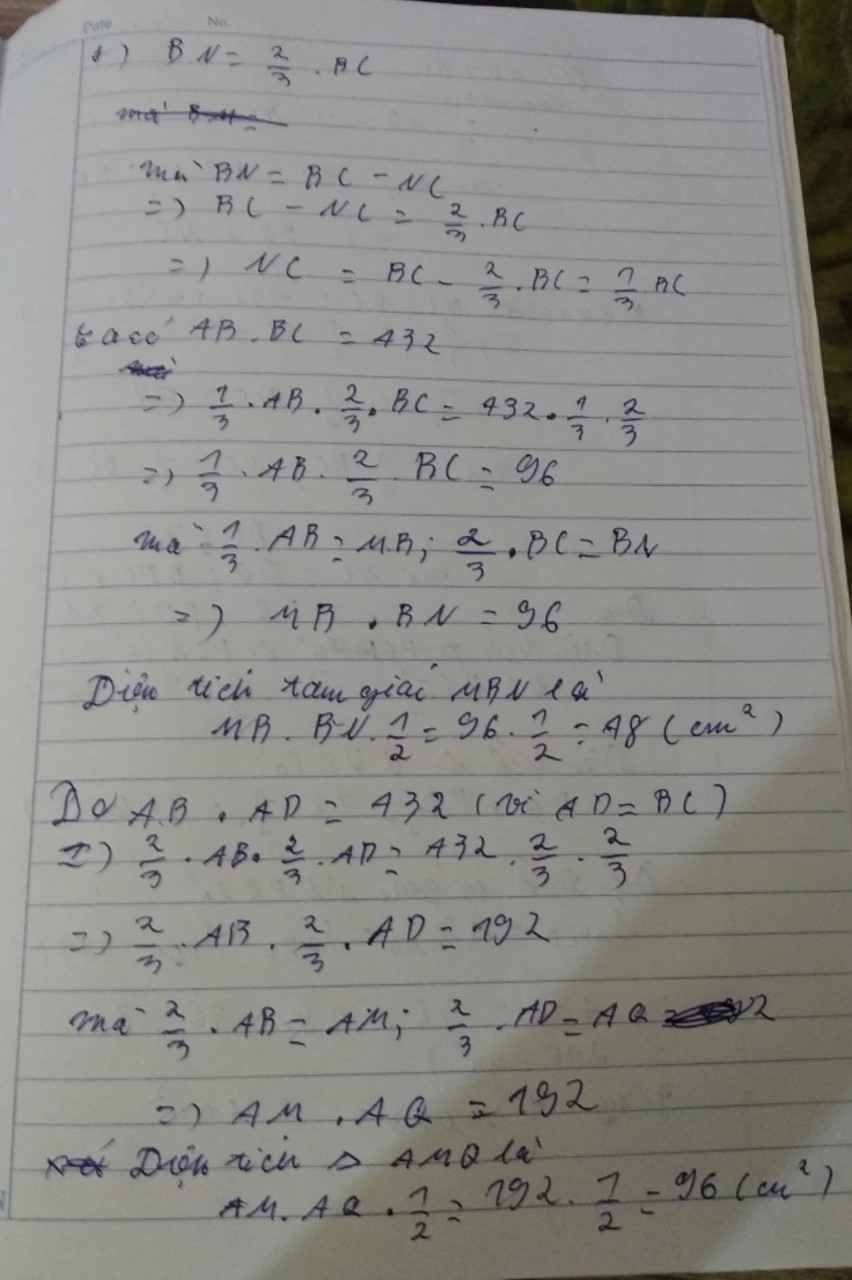

help me
Cô còn đang vẽ hình em ơi.