Lớp 9A đăng kí tham gia vệ sinh trường học, với số lượng đăng kí cô giáo chủ nhiệm dự định chia lớp thành 3 tổ có số học sinh như nhau. Nhưng sau đó lớp có thêm 4 học sinh đăng kí nữa. Do đó, cô giáo chủ nhiệm đã chia đều số học sinh của lớp thành 4 tổ. Hỏi lớp 9A hiện có bao nhiêu học sinh tham gia vệ sinh trường học, biết rằng so với phương án dự định ban đầu, số học sinh của mỗi tổ hiện nay có ít hơn 2 học sinh ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Để pt có 2 nghiệm phân biệt thì:
$\Delta'=m^2-(2m-4)=m^2-2m+4>0$
$\Leftrightarrow (m-1)^2+3>0$
$\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet:
$x_1+x_2=2m$
$x_1x_2=2m-4$
Khi đó:
$x_1+2x_2=8$
$\Leftrightarrow 2m+x_2=8$
$\Leftrightarrow x_2=8-2m$
$\Leftrightarrow x_1=2m-x_2=2m-(8-2m)=4m-8$
$2m-4=x_1x_2=(4m-8)(8-2m)$
$\Leftrightarrow m-2=(2m-4)(8-2m)=2(m-2)(8-2m)$
$\Leftrightarrow (m-2)[2(8-2m)-1]=0$
$\Leftrightarrow (m-2)(15-4m)=0$
$\Leftrightarrow m=2$ hoặc $m=\frac{15}{4}$

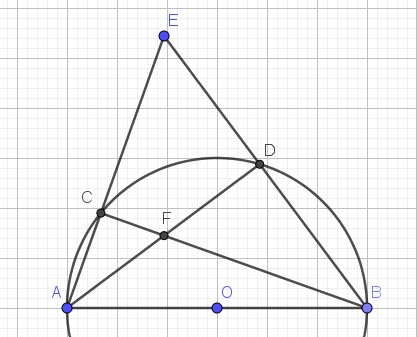
Lời giải:
a.
Ta thấy $\widehat{ACB}=\widehat{ADB}=90^0$ (góc nội tiếp chắn nửa đường tròn)
$\Rightarrow \widehat{ECF}=180^0-\widehat{ACB}=180^0-90^0=90^0$; $\widehat{EDF}=180^0-\widehat{ADB}=180^0-90^0=90^0$
Tứ giác $ECFD$ có tổng 2 góc đối $\widehat{ECF}+\widehat{EDF}=90^0+90^0=180^0$ nên $ECFD$ là tứ giác nội tiếp.
b.
Vì $ECFD$ là tứ giác nội tiếp nên $\widehat{AEF}=\widehat{CEF}=\widehat{CDF}=\widehat{ADC}$ (góc nt chắn cung $CF$)

\(\left\{{}\begin{matrix}4x+y=2\\8x+3y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4.2+2y=2.2\\8x+3y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}8x+2y=4\\8x+3y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-y=-1\\4x+y=2\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}y=1\\4x+1=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{4}\\y=1\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(\dfrac{1}{4};1\right)\)