Cho a thuộc N , b thuộc N , a:8 dư 6 , b:8 dư 2 (a>6)
a) Chứng tỏ a+b chia hết cho 8
b) Tìm số dư của 2a-b :8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ ghép chính phụ: lâu đời, súng trường, nhà máy, nhà trường, thủ môn, cá chép, bút chì.
Từ ghép đẳng lập: suy nghĩ, suy xét, nhà ở, chài lưới, ẩm ướt, tươi tốt, đầu đuôi, cỏ cây, sơn hà, núi đồi.

Bài 2
S = 6 + 6² + 6³ + 6⁴ + ... + 6⁹⁹
6S = 6² + 6³ + 6⁴ + 6⁵ + 6⁹⁹
5S = 6S - S = (6² + 6³ + 6⁴ + 6⁵ + ... + 6¹⁰⁰) - (6 + 6² + 6³ + 6⁴ + ... + 6⁹⁹)
= 6¹⁰⁰ - 6
S = (6¹⁰⁰ - 6)/5
----------------
S = 1/3 + 1/3² + 1/3⁴ + 1/3⁶ + ... + 1/3⁹⁸ + 1/3¹⁰⁰
S/9 = 1/3³ + 1/3⁴ + 1/3⁶ + 1/3⁸ + ... + 1/3¹⁰⁰ + 1/3¹⁰²
-8S/9 = S/9 - S
= (1/3³ + 1/3⁴ + 1/3⁶ + 1/3⁸ + ... + 1/3¹⁰⁰ + 1/3¹⁰²) - (1/3 + 1/3² + 1/3⁴ + 1/3⁶ + ... + 1/3¹⁰⁰)
= 1/3¹⁰² + 1/3³ - 1/3 - 1/3²
= 1/3¹⁰² - 11/27
S = (1/3¹⁰² - 11/27)/(-8/9)
= -1/(8.3¹⁰⁰) + 11/8
--------------------
S = 1 + 4 + 4² + 4³ + ... + 4¹⁰⁰⁰
4S = 4 + 4² + 4³ + 4⁴ + ... + 4¹⁰⁰¹
3S = 4S - S
= (4 + 4² + 4³ + 4⁴ + ... + 4¹⁰⁰¹) - (1 + 4 + 4² + 4³ + ... + 4¹⁰⁰⁰)
= 4¹⁰⁰¹ - 1
S = (4¹⁰⁰¹ - 1)/3
--------------------
S = 1 + 1/2 + 1/2² + 1/2⁴ + ... + 1/2⁹⁸ + 1/2¹⁰⁰
S/4 = 1/2² + 1/2³ + 1/2⁴ + 1/2⁶ + ... + 1/2¹⁰⁰ + 1/2¹⁰²
3S/4 = S - S/4
= (1 + 1/2 + 1/2² + 1/2⁴ + ... + 1/2⁹⁸ + 1/2¹⁰⁰) - (1/2² + 1/2³ + 1/2⁴ + 1/2⁶ + ... + 1/2¹⁰⁰ + 1/2¹⁰²)
= 1 + 1/2 - 1/2³ - 1/2¹⁰²
= 11/8 - 1/2¹⁰²
S = (11/8 - 1/2¹⁰²) : 3/4
= 33/2 - 1/(3.2¹⁰⁰)
Bài 3
a) A = 5⁵ - 5⁴ + 5³
= 5³.(5² - 5 + 1)
= 5³.21 ⋮ 7 (vì 21 ⋮ 7)
Vậy A ⋮ 7
b) B = 10⁶ - 5⁷
= 2⁶.5⁶ - 5⁷
= 5⁶.(2⁶ - 5)
= 5⁶.(64 - 5)
= 5⁶.59 ⋮ 59
Vậy B ⋮ 59
c) C = 81⁷ - 27⁹ - 9¹³
= (3⁴)⁷ - (3³)⁹ - (3²)¹³
= 3²⁸ - 3²⁷ - 3²⁶
= 3²⁴.(3⁴ - 3³ - 3²)
= 3²⁴.(81 - 27 - 9)
= 3²⁴.45 ⋮ 45
Vậy C ⋮ 45
d) D = 10⁹ + 10⁸ + 10⁷
= 10⁷.(10² + 10 + 1)
= 10⁷.(100 + 11)
= 10⁷.111
= 2⁷.5⁷.111
= 2⁶.5⁷.2.111
= 2⁶.5⁷.222 ⋮ 222
D = 2⁷.5⁷.111
= 2⁷.5⁶.5.111
= 2⁷.5⁶.555 ⋮ 555
Vậy D ⋮ 222 và D ⋮ 555
e) E = 16⁵ + 2¹⁵
= (2⁴)⁵ + 2¹⁵
= 2²⁰ + 2¹⁵
= 2¹⁵.(2⁵ + 1)
= 2¹⁵.(32 + 1)
= 2¹⁵.33 ⋮ 33
Vậy E ⋮ 33

Gọi x , y , z là mỗi tổ (người làm):tổ 1, 2, 3(x , y ,z ∈ N*)Gọi x , y , z là mỗi tổ (người làm):tổ 1, 2, 3(x , y ,z ∈ N*)
Tổ 2 hơn tổ 3 là 8 người nên: a - za - z
Vì năng suất mỗi người như nhau nên số người và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịchVì năng suất mỗi người như nhau nên số người và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch
Ta có:Ta có:
2x = 3y = 5z2x = 3y = 5z
=>2x302�30=3y303�30=5y305�30
=>x15�15=y10�10=z6�6=y−z10−6�−�10−6=8484=22
Ta làm phép tính như sau:
=>x15�15=2.152.15=3030
y10�10=2.102.10=2020
z6�6 =2.62.6=1212
Ta kết luận rằng:
Tổ 1 có 30 ngườiTổ 1 có 30 người
Tổ 2 có 20 ngườiTổ 2 có 20 người
Tổ 3 có 12 người
Gọi x , y , z là mỗi tổ (người làm):tổ 1, 2, 3(x , y ,z ∈ N*) Tổ 2 hơn tổ 3 là 8 người nên: a - z Vì năng suất mỗi người như nhau nên số người và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch Ta có: 2x = 3y = 5z => 2 x 30 = 3 y 30 = 5 y 30 => x 15 = y 10 = z 6 = y − z 10 − 6 = 8 4 = 2 Ta làm phép tính như sau: => x 15 = 2.15 = 30 y 10 = 2.10 = 20 z 6 = 2.6 = 12 Ta kết luận rằng: Tổ 1 có 30 người Tổ 2 có 20 người Tổ 3 có 12 người

\(\dfrac{5x-2}{3}=\dfrac{3}{4}\)
\(\Rightarrow4\left(5x-2\right)=9\)
\(\Rightarrow20x-8=9\)
\(\Rightarrow20x=17\)
\(\Rightarrow x=\dfrac{17}{20}\)
Đính chính \(\dfrac{5x-2}{3}=-\dfrac{3}{4}\)
\(\Rightarrow4\left(5x-2\right)=-9\)
\(\Rightarrow20x-8=-9\)
\(\Rightarrow20x=-1\)
\(\Rightarrow x=-\dfrac{1}{20}\)

Sau khi giảm lần 1, chiếc tivi còn giá : 20 000 000 - ( 20 000 000 . 5%)= 19 000 000 ( đồng)
Sau khi giảm lần 2, chiếc tivi còn giá : 19 000 000 - ( 19 000 000 . 2%)= 18 620 000 ( đồng)
Vậy khách hàng phải trả 18 620 000 đồng để mua chiếc tivi
1.
Bài làm:
* Lần giảm giá thứ nhất.
Số tiền khách hàng được giảm là:
\(20000000.\dfrac{5}{100}=1000000\) ( đồng )
Giá của chiếc tivi sau lần giảm thứ nhất là:
\(20000000-1000000=19000000\) ( đồng )
* Lần giảm giá thứ hai.
Số tiền khách hàng được giảm là:
\(19000000.\dfrac{2}{100}=380000\) ( đồng )
Giá của chiếc tivi sau lần giảm thứ hai là:
\(19000000-380000=18620000\) ( đồng )
Vậy khách hàng phải trả 18 620 000 đồng cho chiếc tivi sau 2 lần giảm.

1. has been repairing (nếu còn đang làm)
has repaired (nếu đã nghỉ làm)
2. haven't watched
3. has been increasing

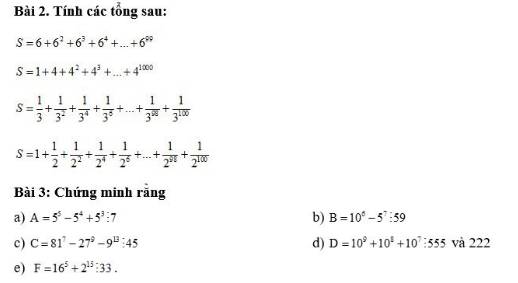
a) Theo đề :
\(a=8m+6\)
\(b=8n+2\) \(\left(m;n\inℕ^∗\right)\)
\(\Rightarrow a+b=8m+8n+8=8\left(m+n+1\right)⋮8\)
\(\Rightarrow dpcm\)
b) \(2a-b=2\left(8m+6\right)-\left(8n+2\right)\)
\(\Rightarrow2a-b=16m+12-8n-2\)
\(\Rightarrow2a-b=16m-8n+10\)
\(\Rightarrow2a-b=16m-8n+8+2\)
\(\Rightarrow2a-b=8\left(2m-n+1\right)+2\)
\(\Rightarrow2a-b:8\) dư \(2\)