Biết hình chữ nhật có chiều dài gấp tám lần chiều rộng. Biểu thức tính diện tích hình chữ nhật khi chiều rộng bằng Unexpected text node: 'x'Unexpected text node: 'x'x là

Biểu thức : 8x²

*Sxl

\(Ta\) \(có\) \(biểu\) \(thức\) \(sau:\)

\(x\)\(.\) \(x\) \(.\) \(8\) =  \(S\)

          \(-\) \(Hok\) \(T\) \(-\)

\(x^3-6x^2y+12xy^2-8y^3\)

\(=\left(x-2y\right)^3\)

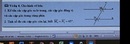
1 Các cặp góc so le trong là : góc M3 và N1; N2 và M4.                        Các cặp góc đồng vị là : M1 và N1; M2 và N2; M3 và N3; M4 và N4

Các cặp góc trong cùng phía là : M3 và N2; M4 và N1. 

ta có 

\(M=\frac{xy+x+4+1}{xy+x+4}=1+\frac{1}{xy+x+4}\) nguyên khi

\(\orbr{\begin{cases}xy+x+4=1\\xy+x+4=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x\left(y+1\right)=-3\\x\left(y+1\right)=-5\end{cases}}}\)

TH1:\(x\left(y+1\right)=-3\Rightarrow x\in\left\{-3,-1,1,3\right\}\text{ tương ứng }y\in\left\{0,2,-4,-2\right\}\)

TH2:\(x\left(y+1\right)=-5\Rightarrow x\in\left\{-5,-1,1,5\right\}\text{ tương ứng }y\in\left\{0,4,-6,-2\right\}\)

Ta có \(M=\frac{xy+x+5}{xy+x+4}=\frac{xy+x+4+1}{xy+x+4}=1+\frac{1}{xy+x+4}\)

\(M\inℤ\Leftrightarrow1⋮xy+y+4\)

=> \(xy+y+4\inƯ\left(1\right)\)

=> \(xy+y+4\in\left\{1;-1\right\}\)

=> \(xy+y\in\left\{-3;-5\right\}\)

Khi xy + x = -3

=> x(y + 1) = -3 

Lập bảng xét các trường hợp 

Nếu xy + x = -5

=> x(y + 1) = -5

Lập bảng xét các trường hợp 

Vậy các cặp (x;y) thỏa mãn là (1;-4) ; (-1 ; 2) ; (3 ; -2) ; (-3 ; 0) ; (1 ;- 6) ; (-5 ; 0) ; (5 ; -2) ; (-1;4) 

 A = 2x²y - 8xy² + 4x³y³ +9xy² - x²y - 5x³y³

=-x³y³+x²y+xy²

^HT

\(\frac{4x^2+9}{x^2+1}\)

\(=\frac{4\left(x^2+1\right)+5}{x^2+1}\)

\(=\frac{4\left(x^2+1\right)}{x^2+1}+\frac{5}{x^2+1}\)

để \(\frac{4x^2+9}{x^2+1}\) lớn nhất thì \(\frac{5}{x^2+1}\) phải lớn nhất => x²+1 phải nhỏ nhất =>\(x=\pm1\)

=>\(\frac{4x^2+9}{x^2+1}=\frac{13}{2}\)(6,5)