\(\dfrac{2}{11}-\left(\dfrac{-5}{11}+\dfrac{12}{11}\right)\)

\(=\dfrac{2}{11}-\dfrac{-5+12}{11}\)

\(=\dfrac{2}{11}-\dfrac{7}{11}\) 

\(=\dfrac{2-7}{11}\)

\(=\dfrac{-5}{11}\)

= 2/11- 7/11

=-5/11

Để \(\dfrac{3}{n+2}\) là phân số tối giản thì: 

n + 2 không chia hết 3 

\(\Rightarrow n+2\) ≠ B(3) 

Đặt B(3) = 3k (k ∈ Z)  

\(\Rightarrow n+2\) ≠ 3k 

⇒ n ≠ 3k - 2 

⇒ Chọn C 

a: Xét ΔOAB và ΔOCD có

\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)

\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)

Do đó: ΔOAB~ΔOCD

b: Sửa đề: cắt BC tại N

Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\)

=>\(OM\cdot AC=DC\cdot AO\)

c: Xét ΔADC có OM//DC

nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\)(1)

Xét ΔBDC có ON//DC

nên \(\dfrac{ON}{DC}=\dfrac{BO}{BD}\left(2\right)\)

Ta có: ΔOAB~ΔOCD

=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)

=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)

=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)

=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)

=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\left(3\right)\)

Từ (1),(2),(3) suy ra OM=ON

=>O là trung điểm của MN

Câu 3: A

Câu 4: D

Câu 15: C

Câu 14: A

Câu 13: C

Câu 12: C

Câu 11: C
Câu 9: D

Câu 8: C

Câu 7: A

                      Bài 1:

   a; Trong hình vẽ trên có những tia: 

 CE; CK; Ct; Cn; Ex; Em; En; Ey; Kx; Kt; Ky

   Trong hình vẽ có những đoạn thẳng là:

          CE; CK; EK

b; Các cặp tia đối nhau là:

         Ct Và Ck; CE và Cn; Ex và Ek; Ex và Ey; Ky và Kx; Ky và KE

Bài 2:a;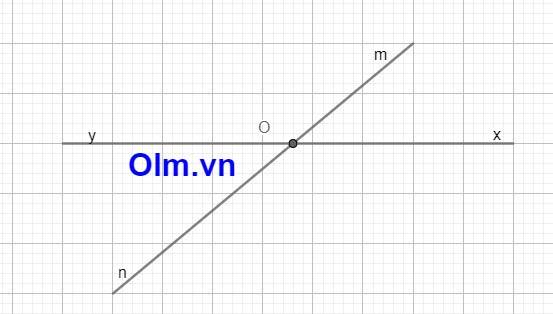 

Các tia đối nhau là:

On và Om; Ox và Oy

\(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+\dfrac{2}{9\cdot11}+\dfrac{2}{11\cdot13}\)

\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}\)

\(=\dfrac{1}{3}-\dfrac{1}{13}\)

\(=\dfrac{13}{39}-\dfrac{3}{39}\)

\(=\dfrac{10}{39}\)

\(\left(\dfrac{7}{30}\cdot\dfrac{12}{37}+\dfrac{12}{30}\cdot\dfrac{23}{37}\right)\cdot\dfrac{13}{31}-\dfrac{-25}{37}\cdot\dfrac{18}{31}\)

\(=\left(\dfrac{7}{30}\cdot\dfrac{12}{37}+\dfrac{12}{37}\cdot\dfrac{23}{30}\right)\cdot\dfrac{13}{31}+\dfrac{25}{37}\cdot\dfrac{18}{31}\)

\(=\dfrac{12}{37}\cdot\left(\dfrac{7}{30}+\dfrac{23}{30}\right)\cdot\dfrac{13}{31}+\dfrac{25}{37}\cdot\dfrac{18}{31}\)

\(=\dfrac{12}{37}\cdot1\cdot\dfrac{13}{31}+\dfrac{18}{37}\cdot\dfrac{25}{31}\)

\(=\dfrac{6}{37}\cdot\dfrac{26}{31}+\dfrac{6}{37}\cdot\dfrac{75}{31}\)

\(=\dfrac{6}{37}\cdot\left(\dfrac{26}{31}+\dfrac{75}{31}\right)\)

\(=\dfrac{6}{37}\cdot\dfrac{101}{31}\)

\(=\dfrac{606}{1147}\)

a: Để \(\dfrac{1}{n+3}\) min thì n+3=-1

=>n=-4

=>\(\dfrac{1}{n+3}_{min}=\dfrac{1}{-4+3}=-1\)

b: \(\dfrac{8-x}{x-3}=\dfrac{-x+3+5}{x-3}=-1+\dfrac{5}{x-3}\)

Để \(\dfrac{8-x}{x-3}_{min}\) thì x-3=-1

=>x=2

=>GTNN là \(\dfrac{8-2}{2-3}=\dfrac{6}{-1}=-6\)

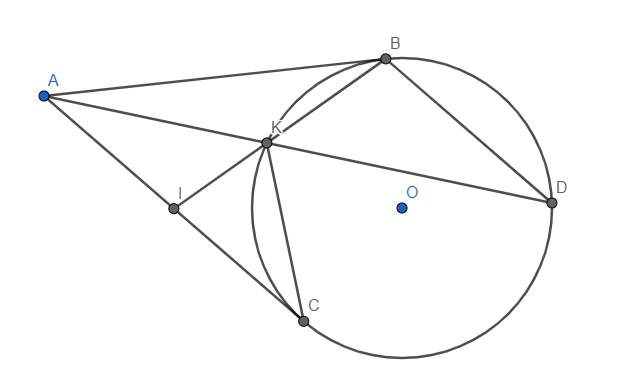
b) Do BD//AC nên \(\widehat{KAI}=\widehat{KDB}\) (2 góc so le trong)

 Lại có \(\widehat{ABI}=\widehat{ABK}=\widehat{BDK}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BK.

 \(\Rightarrow\widehat{KAI}=\widehat{KBA}\)

c) I là trung điểm AC chứ không phải BC nhé.

 Xét tam giác IAK và IBA, ta có:

 \(\widehat{AIB}\) chung, \(\widehat{IAK}=\widehat{IBA}\left(cmt\right)\) 

 \(\Rightarrow\Delta IAK\sim\Delta IBA\left(g.g\right)\)

 \(\Rightarrow\dfrac{IA}{IB}=\dfrac{IK}{IA}\)

 \(\Rightarrow IA^2=IB.IK\)

 \(\Rightarrow IA=IC\) (vì theo câu a, \(IC^2=IB.IK\))

 \(\Rightarrow\) I là trung điểm AC.

d) CK vuông góc với đường nào trong đề bài chưa nói nhé.