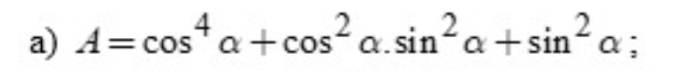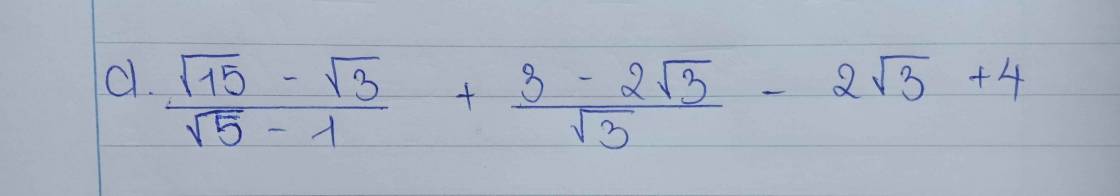Bài 1 :

a) \(Cos30^o=Cos\left(2.15^o\right)=2cos^215^o-1\)

\(\Rightarrow cos^215^o=\dfrac{cos30^o+1}{2}\)

\(\Rightarrow cos^215^o=\dfrac{\dfrac{\sqrt[]{3}}{2}+1}{2}\)

\(\Rightarrow cos^215^o=\dfrac{\sqrt[]{3}+2}{4}\)

\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\sqrt[]{3}+2}}{2}\)

\(\Rightarrow cos15^o=\dfrac{2\sqrt[]{\sqrt[]{3}+2}}{4}\)

\(\Rightarrow cos15^o=\dfrac{\sqrt[]{4\sqrt[]{3}+8}}{4}\)

\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6+2.2\sqrt[]{2}\sqrt[]{6}+2}}{4}\)

\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\left(\sqrt[]{6}+\sqrt[]{2}\right)^2}}{4}\)

\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6}+\sqrt[]{2}^{ }}{4}\left(dpcm\right)\)

a)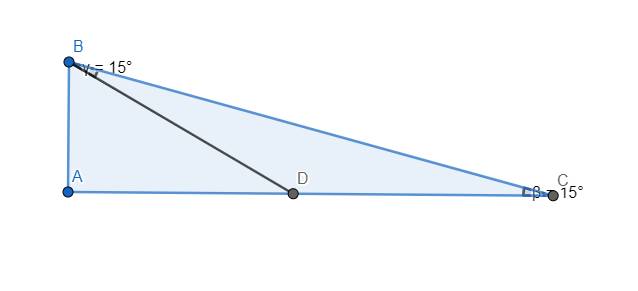

 Dựng tam giác ABC vuông tại A với \(\widehat{C}=15^o\). Trên đoạn thẳng AC lấy điểm D sao cho \(\widehat{CBD}=15^o\). Không mất tính tổng quát, ta chuẩn hóa \(AB=1\). \(\Rightarrow\left\{{}\begin{matrix}BD=\dfrac{AB}{cos60^o}=2\\AD=AB.tan60^o=\sqrt{3}\end{matrix}\right.\)

 Dễ thấy tam giác DBC cân tại D \(\Rightarrow BD=CD=2\) \(\Rightarrow AC=AD+DC=2+\sqrt{3}\)

  \(\Rightarrow tanC=\dfrac{AB}{AC}=\dfrac{1}{2+\sqrt{3}}=2-\sqrt{3}\) 

\(\Rightarrow\dfrac{sinC}{cosC}=2-\sqrt{3}\)

\(\Rightarrow sinC=\left(2-\sqrt{3}\right)cosC\)

Mà \(sin^2C+cos^2C=1\)

\(\Rightarrow\left(7-4\sqrt{3}\right)cos^2C+cos^2C=1\)

\(\Leftrightarrow\left(8-4\sqrt{3}\right)cos^2C=1\)

\(\Leftrightarrow cos^2C=\dfrac{1}{8-4\sqrt{3}}=\dfrac{2+\sqrt{3}}{4}\)

\(\Leftrightarrow cosC=\sqrt{\dfrac{2+\sqrt{3}}{4}}\) \(=\dfrac{\sqrt{2+\sqrt{3}}}{2}=\dfrac{\sqrt{8+4\sqrt{3}}}{4}\) \(=\dfrac{\sqrt{6}+\sqrt{2}}{4}\) 

\(\Rightarrow cos15^o=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)

\(a_1,\sqrt{x}< 7\\ \Rightarrow x< 49\\ a_2,\sqrt{2x}< 6\\ \Rightarrow x< 18\\ a_3,\sqrt{4x}\ge4\\ \Rightarrow4x\ge16\\ \Rightarrow x\ge4\\ a_4,\sqrt{x}< \sqrt{6}\\ \Rightarrow x< 6\)

\(b_1,\sqrt{x}>4\\ \Rightarrow x>16\\ b_2,\sqrt{2x}\le2\\ \Rightarrow2x\le4\\ \Rightarrow x\le2\\ b_3,\sqrt{3x}\le\sqrt{9}\\ \Rightarrow3x\le9\\ \Rightarrow x\le3\\ b_4,\sqrt{7x}\le\sqrt{35}\\ \Rightarrow7x\le35\\ \Rightarrow x\le5\)

\(A=2+2^2+...2^{2021}\)

\(\Rightarrow A+1=1+2+2^2+...2^{2021}\)

\(\Rightarrow A+1=\dfrac{2^{2021+1}-1}{2-1}\)

\(\Rightarrow A+1=2^{2022}-1\)

\(\Rightarrow A=2^{2022}-2< 2^{2022}=B\)

\(\Rightarrow A< B\)

Gọi số cần tìm là ab

Theo bài ra ta có:

\(ab3-ab=750\)

\(\Rightarrow abx10+3-abx1=750\)

\(\Rightarrow abx9+3=750\)

\(\Rightarrow abx9=750-3=747\)

\(\Rightarrow ab=747:9=83\)

Vậy số cần tìm là 83

Bạn xem kỹ lại đề có đúng không?

Lời giải:
Áp dụng BĐT Bunhiacopxky:

$\text{VT}(1^2+1^2+1^2)\geq (1+\frac{x}{y+z}+1+\frac{y}{x+z}+1+\frac{z}{x+y})^2$

$\Leftrightarrow 3\text{VT}\geq (3+\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y})^2$

$ = \left[3+\frac{x^2}{xy+xz}+\frac{y^2}{yz+yx}+\frac{z^2}{zy+zx}\right]^2$

$\geq \left[3+\frac{(x+y+z)^2}{2(xy+yz+xz)}\right]^2$

$\geq \left[3+\frac{3(xy+yz+xz)}{2(xy+yz+xz)}\right]^2=\frac{81}{4}$

$\Rightarrow \text{VT}\geq \frac{27}{4}$

Dấu "=" xảy ra khi $x=y=z>0$

Áp dụng BĐT Bunhiacopxky:

$\text{VT}(1^2+1^2+1^2)\ge (1+\genfrac{}{}{0ex}{}{x}{y+z}+1+\genfrac{}{}{0ex}{}{y}{x+z}+1+\genfrac{}{}{0ex}{}{z}{x+y}{)}^2$

$\iff 3\text{VT}\ge (3+\genfrac{}{}{0ex}{}{x}{y+z}+\genfrac{}{}{0ex}{}{y}{x+z}+\genfrac{}{}{0ex}{}{z}{x+y}{)}^2$

$={\left[3+\genfrac{}{}{0ex}{}{x^2}{xy+xz}+\genfrac{}{}{0ex}{}{y^2}{yz+yx}+\genfrac{}{}{0ex}{}{z^2}{zy+zx}\right]}^2$

$\ge {\left[3+\genfrac{}{}{0ex}{}{(x+y+z{)}^2}{2(xy+yz+xz)}\right]}^2$

$\ge {\left[3+\genfrac{}{}{0ex}{}{3(xy+yz+xz)}{2(xy+yz+xz)}\right]}^2=\genfrac{}{}{0ex}{}{81}{4}$

$\Rightarrow \text{VT}\ge \genfrac{}{}{0ex}{}{27}{4}$

Dấu "=" xảy ra khi $x=y=z>0$