Câu 1: Một hình thoi có diện tích là 40dm2, độ dài một đường chéo là 8dm. Độ dài đường chéo còn lại là:
A) 5dm
B) 10dm
C) 320dm
D) 260dm
Câu 2: Tìm số tự nhiên x biết: 5x + 3x = 88
A) x = 11
B) x = 5
C) x = 8
D) Một kết quả khác
Câu 3: Số phần tử của tập hợp D = {1; 3; 5; 7; ...; 999} là:
A) 999
B) 998
C) 500
D) 499
Câu 4: Số hình thoi trong hình vẽ là:
A) 0
B) 1
C) 2
D) 3
Câu 5: Khẳng định nào sau đây...
Đọc tiếp
Câu 1: Một hình thoi có diện tích là 40dm2, độ dài một đường chéo là 8dm. Độ dài đường chéo còn lại là:
A) 5dm
B) 10dm
C) 320dm
D) 260dm
Câu 2: Tìm số tự nhiên x biết: 5x + 3x = 88
A) x = 11
B) x = 5
C) x = 8
D) Một kết quả khác
Câu 3: Số phần tử của tập hợp D = {1; 3; 5; 7; ...; 999} là:
A) 999
B) 998
C) 500
D) 499
Câu 4: Số hình thoi trong hình vẽ là:
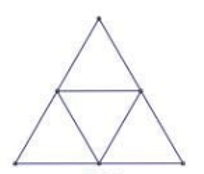
A) 0
B) 1
C) 2
D) 3
Câu 5: Khẳng định nào sau đây đầy đủ nhất cho câu hỏi: “Hình chữ nhật có?”
A) Các cạnh đối song song và bằng nhau
B) Có hai đường chéo bằng nhau.
C) Có bốn góc vuông.
D) Tất cả các ý trên.
II. Tự luận
Bài 1 (2 điểm): Thực hiện phép tính
a) 37.24 + 37.76 + 63.79 + 21.63
b) 101 + (-60) + 29 + (-40)
c) 40 + (139 – 172 + 99) – (139 + 199 – 127)
d) (158.129 – 158.39):180
Bài 2 (2 điểm): Tìm x
a) 25 – 3.(6 – x) = 22
b) [(2x – 11):3 + 1].5 = 20
c) (25 - 2x)3 : 5 - 32 = 42
d) 2.3x = 10.312 + 8.274
Bài 3 (2 điểm): Cô giáo chủ nhiệm muốn chia 120 quyển vở, 48 bút chì và 60 tập giấy thành một số phần thưởng như nhau để thưởng cho học sinh nhân dịp tổng kết học kì I. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng? Mỗi phần thưởng có bao nhiêu quyển vở, bao nhiêu bút chì, bao nhiêu tập giấy?
Bài 4 (1 điểm): Tính chu vi và diện tích hình chữ nhật có chiều dài là 15m và chiều rộng là 8m.


Bài 4:
Chu vi hình chữ nhật là:
(15+8)x2=46(m)
Diện tích hình chữ nhật là:
15x8=120(m2)
Bài 3:
\(120=2^3\cdot3\cdot5;48=2^4\cdot3;60=2^2\cdot3\cdot5\)
=>\(ƯCLN\left(120;48;60\right)=2^2\cdot3=12\)
=>Số phần quà nhiều nhất có thể chia được là 12 phần
Số quyển vở ở mỗi phần là:
120:12=10(quyển)
Số bút chì ở mỗi phần là:
48:12=4(cây)
Số tập giấy ở mỗi phần là:
60:12=5(tập)