Gọi số học sinh lớp 6C là x,( xϵ N , x≠ 0)

Ta có: \(3=3\\ 5=5\\ 9=3^2\) 

\(\Rightarrow BCNN\left(3,5,9\right)=3^2.5=45\)

\(\Rightarrow B\left(45\right)=\left\{0;45;90;135;...\right\}\)

Mà \(35< x< 60\\ \Rightarrow x=45.\)

Vậy lớp 6C có 45 học sinh.

Nhanh với cứu toiii

3n + 9 chia hết cho n ( n khác 0 ) 

Vì 3n chia hết cho n với mọi n là STN khác 0

=> 9 chia hết cho n 

Hay n thuộc Ư(9)={1;3;9}

Tổng = 13

5\(^{x+1}\) - 5\(^x\) = 2.2⁸ + 8

5\(^x\).(5 - 1) = 520

5\(^x\).4        = 520

5\(^x\)           = 520 : 4

5\(^x\)           = 130

Với \(x\) = 0 ⇒ 5\(^x\) = 5⁰ = 1 < 130 (loại)

Với \(x\) > 0 ⇒ 5\(^x\) = \(\overline{...5}\) \(\ne\) 130 (loại)

Vậy \(x\) \(\in\) \(\varnothing\) 

\(5^{x+1}-5^x=2.2^8+8\\ 5^x\left(5-1\right)=512+8\\ 5^x.4=520\\ 5^x=\dfrac{520}{4}=130\)

Em xem lại đề

Gọi số học sinh là \(a\) (học sinh)

Ta có: \(a⋮9,12,15\) và \(500\le a\le550\)

⇒ \(a\in B\left(9,12,15\right)\)

\(B\left(9,12,15\right)=\left\{0,180,360,540,720,...\right\}\)

⇒ \(a=540\)

Vậy số học sinh khối 6 của trường đó là 540 học sinh

\(17\times45-45\times2+15\times55\)

\(=45\times\left(17-2\right)+15\times55\)

\(=45\times15+15\times55\)

\(=15\times\left(45+55\right)\)

\(=15\times100\)

\(=1500\)

Giúp tớ nhanh với ạ

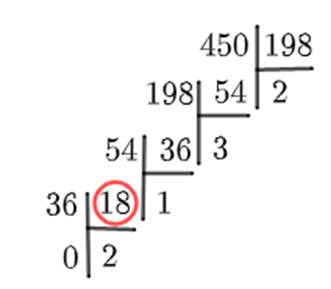
OLM, giải thích chỗ em khoanh đỏ nhá 54 : 36 = 1 dư 18 em nhé

156 = 2².3.13

169 = 13²

130 = 2.5.13

ƯCLN(156; 169; 130) = 13 

 Trước tiên, ta cần chứng minh 2 bổ đề sau:

 Bổ đề 1: Cho 2 số tự nhiên \(a,b\) khác 0. Khi đó  \(ƯCLN\left(a,b\right).BCNN\left(a,b\right)=a.b\). 

 Bổ đề 2: Cho 2 số tự nhiên \(a,b\) khác 0. Khi đó:\(ƯCLN\left(a,b\right)+BCNN\left(a,b\right)\ge a+b\)

 Chứng minh:

 Bổ đề 1: Đặt \(\left(a,b\right)=1\) (từ nay ta sẽ kí hiệu \(\left(a,b\right)=ƯCLN\left(a,b\right)\) và \(\left[a;b\right]=BCNN\left(a,b\right)\) cho gọn) \(\Rightarrow\left\{{}\begin{matrix}a=dk\\b=dl\end{matrix}\right.\left(\left(k,l\right)=1\right)\)

  Nên \(\left[a,b\right]=dkl\) \(\Rightarrow\left(a;b\right)\left[a;b\right]=dk.dl=ab\). Ta có đpcm.

 Bổ đề 2: Vẫn giữ nguyên kí hiệu như ở chứng minh bổ đề 1. Ta có \(k\ge1,l\ge1\) nên \(\left(k-1\right)\left(l-1\right)\ge0\)

 \(\Leftrightarrow kl-k-l+1\ge0\)

 \(\Leftrightarrow kl+1\ge k+l\)

 \(\Leftrightarrow dkl+d\ge dk+dl\)

 \(\Leftrightarrow\left[a,b\right]+\left(a,b\right)\ge a+b\) (đpcm)

Vậy 2 bổ đề đã được chứng minh.

a) Áp dụng bổ đề 1, ta có \(ab=\left(a,b\right)\left[a,b\right]=15.180=2700\) và \(a+b\le\left(a,b\right)+\left[a,b\right]=195\). Do \(b\ge a\) \(\Rightarrow a^2\le2700\Leftrightarrow a\le51\)

 Mà \(15|a\) nên ta đi tìm các bội của 15 mà nhỏ hơn 51:

  \(a\in\left\{15;30;45\right\}\)

 Khi đó nếu \(a=15\) thì \(b=180\) (thỏa)

 Nếu \(a=30\) thì \(b=90\) (loại)

 Nếu \(a=45\) thì \(b=60\) (thỏa)

 Vậy có 2 cặp số a,b thỏa mãn ycbt là \(15,180\) và \(45,60\)

Câu b làm tương tự.

 Ko bt

B

Số liền trước của số a+1 là:

a+1 - 1= a

Chọn B

a=73

N=40+4

N=20+2