Quy đồng các phân thức sau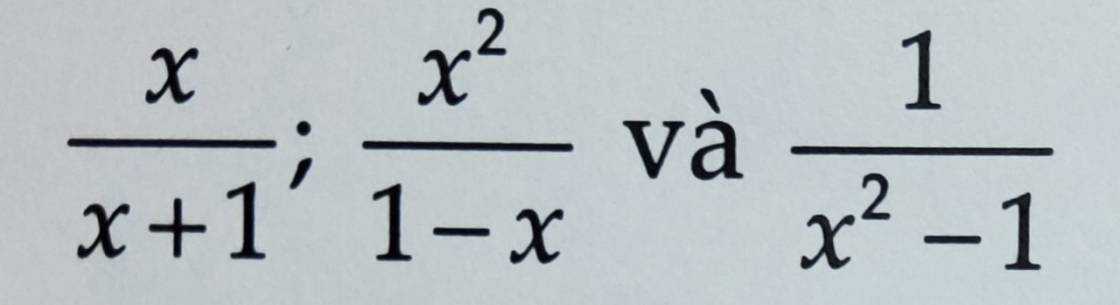
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số có 4 chữ số thỏa mãn là \(\overline{abcd}\). Khi đó a có 4 cách chọn (từ 1 đến 4). Còn các chữ số b, c, d đều có 5 cách chọn (từ 0 đến 4). Do đó có tất cả \(4.5.5.5=500\) số thỏa mãn ycbt.

Bài 10
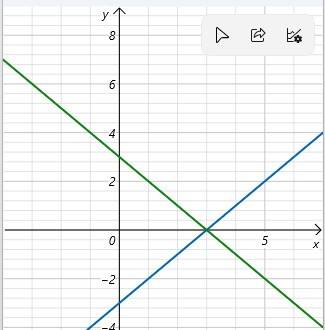
a; Giao của d1 với trục ox là điểm có hoành độ thỏa mãn
\(x\) - 3 = 0 ⇒ \(x\) = 3
Giao của d1 với trục oy là điểm có tung độ thỏa mãn y = 0 - 3 = -3
Giao của d2 với trục ox là điểm có hoành độ thỏa mãn
3 - \(x\) = 0 ⇒ \(x\) = 3
Giao của d2 với trục oy là điểm có tung độ thỏa mãn y = 3 - 0 = 3
Ta có đồ thị d1 và d2 như hình dưới
b; Giao của d1 và d2 là điểm có phương trình hoành độ thỏa mãn
\(x\) - 3 = 3 - \(x\)
2\(x\) = 6
\(x\) = 6 : 2
\(x\) = 3; ⇒ y = 3- 3 =0
Vậy giao của d1 và d2 là A(3;0)
Bài 9:
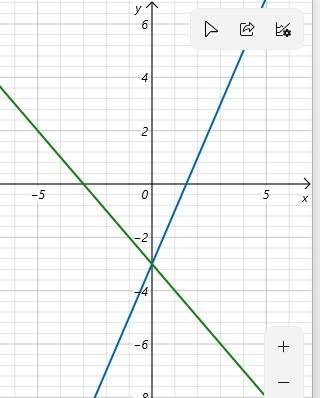
Giao của d1 với trục ox là điểm có hoành độ thỏa mãn
2\(x\) - 3 = 0 ⇒ \(x\) = \(\dfrac{3}{2}\)
Giao của d1 với trục oy là điểm có tung độ thỏa mãn
y = 2.0 - 3 = - 3
Giao của d2 với trục ox là điểm có hoành độ thỏa mãn
-3 - \(x\) = 0 ⇒ \(x\) = 0
Giao của d2 với trục oy là điểm có tung độ thỏa mãn
y = -3 - 0 = -3
Ta có đồ thị như hình dưới đây
Giao của d1 và d2 là điểm có hoành độ thỏa mãn phương trình
2\(x\) - 3 = -3 - \(x\)
2\(x\) + \(x\) = 0
3\(x\) =0
\(x\) = 0
⇒ y = -3 - 0
y = - 3
Vậy giao của d1 và d2 là điểm B(0; -3)

\(\dfrac{1}{x-3}+\dfrac{3x^2-8x+10}{x^2-5x+6}-\dfrac{2x-4}{x-2}\left(ĐK:x\ne3;x\ne2\right)\)
\(=\dfrac{1}{x-3}+\dfrac{3x^2-8x+10}{x\left(x-2\right)-3\left(x-2\right)}-\dfrac{2x-4}{x-2}\)
\(=\dfrac{1}{x-3}+\dfrac{3x^2-8x+10}{\left(x-3\right)\left(x-2\right)}-\dfrac{2x-4}{x-2}\)
\(=\dfrac{x-2}{\left(x-2\right)\left(x-3\right)}+\dfrac{3x^2-8x+10}{\left(x-3\right)\left(x-2\right)}-\dfrac{\left(2x-4\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x-2+3x^2-8x+10-\left(2x^2-6x-4x+12\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{3x^2-7x+8-2x^2+10x-12}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x^2+3x-4}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x^2+3x-4}{x^2-5x+6}\)

Áp dụng BĐT trị tuyệt đối:
\(M=\left|x-2019\right|+\left|2021-x\right|+2020\left|x-2020\right|\)
\(M\ge\left|x-2019+2021-x\right|+2020\left|x-2020\right|=2+2020\left|x-2020\right|\ge2\)
\(\Rightarrow M_{min}=2\) khi \(\left\{{}\begin{matrix}\left(x-2019\right)\left(2021-x\right)\ge0\\\left|x-2020\right|=0\end{matrix}\right.\) \(\Rightarrow x=2020\)

a=\(\dfrac{x^2-2x+1-4}{x^2+2x+1}\)=\(\dfrac{\left(x^2-2x+1\right)-4}{x^2+2x+1}\)=\(\dfrac{\left(x-1\right)^2-4}{\left(x+1\right)^2}\)
=\(\dfrac{\left(x-1-2\right)\left(x-1+2\right)}{\left(x+1\right)^2}\)=\(\dfrac{x-3}{x+1}\)
Ta có 3x-1=0
=> 3x=1
=> x=\(\dfrac{1}{3}\)
thay số(...)

a,
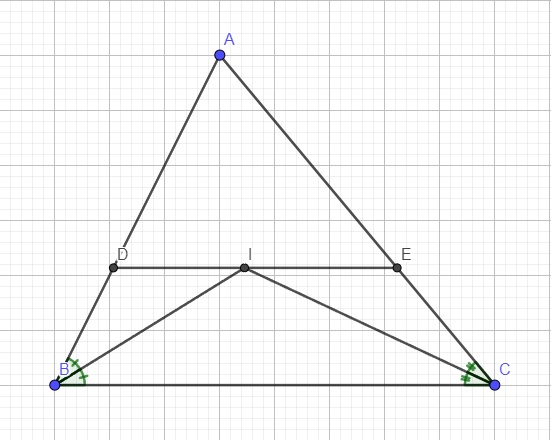
Do \(DE||BC\) (gt) \(\Rightarrow BDEC\) là hình thang
Do \(DE||BC\Rightarrow DI||BC\Rightarrow BDIC\) là hình thang
Do \(DE||BC\Rightarrow IE||BC\Rightarrow BIEC\) là hình thang
b.
Do \(DI||BC\Rightarrow\widehat{CBI}=\widehat{BID}\) (so le trong)
Mà \(\widehat{CBI}=\widehat{DBI}\) (do BI là phân giác góc B)
\(\Rightarrow\widehat{DBI}=\widehat{BID}\)
\(\Rightarrow\Delta BDI\) cân tại D
Tương tự ta có \(\widehat{ICB}=\widehat{CIE}\) (so le trong) và \(\widehat{ICB}=\widehat{ICE}\) (do IC là phân giác góc C)
\(\Rightarrow\widehat{CIE}=\widehat{ICE}\Rightarrow\Delta IEC\) cân tại E
c.
Từ câu b, do \(\Delta BDI\) cân \(\Rightarrow DB=DI\)
Do \(\Delta IEC\) cân \(\Rightarrow IE=CE\)
\(\Rightarrow BD+CE=DI+IE=DE\left(đpcm\right)\)

\(\dfrac{x}{x+1}=\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-x}{x^2-1}\)
\(\dfrac{x^2}{1-x}=\dfrac{-x^2}{x-1}=\dfrac{-x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{-x^3-x^2}{x^2-1}\)