Olm hay quá
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

\(\frac{13}{50}\) giờ + 9% giờ + 24,6 phút + 14,4 phút
= 15,6 giờ + 5,4 phút + 24,6 phút + 14,4 phút
= (15 giờ 36 phút+14,4 phút)+(5,4 phút + 24,6 phút)
= 15 giờ 50,4 phút + 30 phút
= 15 giờ 80,4 phút
= 16 giờ 20 phút 24 giây

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

Giải:
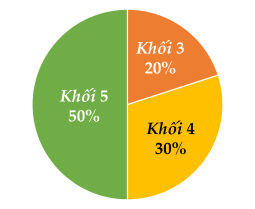
Số học sinh khối 4 tham gia câu lạc bộ là:
60 x 30 : 100 = 18 (học sinh)
Chọn 18 học sinh

\(x^2+2,5x+5\)
\(=x^2+2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}+\dfrac{55}{16}\)
\(=\left(x+\dfrac{5}{4}\right)^2+\dfrac{55}{16}>=\dfrac{55}{16}>0\forall x\)
=>ĐPCM

Olm chào em, đây là toán nâng cao chuyên đề bài toán về công việc, cấu trúc thi chuyên, thi học sinh giỏi các cấp.
Giải:
Một người sẽ làm xong công việc sau số ngày là:
8 x 4 = 32 (ngày)
32 ngày gấp 2 ngày số lần là:
32 : 2 = 16(lần)
Muốn hoàn thành công việc trong 2 ngày thì cần số người là:
1 x 16 = 16 (người)
Đáp số: 16 người
Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!