 giúp em bài 3 và ý c bài 2 ạ
giúp em bài 3 và ý c bài 2 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{2}{3}x\left(x^2-4\right)=0\)
=>\(x\left(x-2\right)\left(x+2\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
b: \(\left(x+2\right)^2-\left(x-2\right)\left(x+2\right)=0\)
=>\(\left(x+2\right)\left(x+2-x+2\right)=0\)
=>4(x+2)=0
=>x+2=0
=>x=-2
c: \(6x^3+7x^2+2x=0\)
=>\(x\left(6x^2+7x+2\right)=0\)
=>\(x\left(6x^2+4x+3x+2\right)=0\)
=>\(x\left(3x+2\right)\left(2x+1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\3x+2=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{2}{3}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
d: \(x^2+4x=7\)
=>\(x^2+4x+4=11\)
=>\(\left(x+2\right)^2=11\)
=>\(\left[{}\begin{matrix}x+2=\sqrt{11}\\x+2=-\sqrt{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{11}-2\\x=-\sqrt{11}-2\end{matrix}\right.\)

\(x+3y=5\Rightarrow x=5-3y\)
Ta có:
\(A=x^2+y^2+16y+2x\)
\(A=\left(5-3y\right)^2+y^2+16y+2\left(5-3y\right)\)
\(A=25-30y+9y^2+y^2+16y+10-6y\)
\(A=10y^2-20y+10+25\)
\(A=10\left(y-1\right)^2+25\ge5\forall y\)
Dấu "=" xảy ra khi \(y=1\Rightarrow x=2\)
Vậy \(A_{min}=25\) khi \(x=2\) và \(y=1\)


a: Sửa đề; \(x^2+x+\dfrac{1}{4}=\dfrac{9}{4}\)
=>\(x^2+x+\dfrac{1}{4}-\dfrac{9}{4}=0\)
=>\(x^2+x-2=0\)
=>(x+2)(x-1)=0
=>\(\left[{}\begin{matrix}x+2=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
b: \(25x^2-16\left(x+2\right)^2=0\)
=>\(\left(5x\right)^2-\left(4x+8\right)^2=0\)
=>\(\left(5x-4x-8\right)\left(5x+4x+8\right)=0\)
=>(x-8)(9x+8)=0
=>\(\left[{}\begin{matrix}x-8=0\\9x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-\dfrac{8}{9}\end{matrix}\right.\)

a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(DP=PC=\dfrac{DC}{2}\)
mà AB=CD
nên AM=MB=DP=PC
Ta có: \(AQ=QD=\dfrac{AD}{2}\)
\(BN=NC=\dfrac{BC}{2}\)
mà AD=BC
nên AQ=QD=BN=NC
Xét ΔAQM vuông tại A và ΔCNP vuông tại C có
AQ=CN
AM=CP
Do đó: ΔAQM=ΔCNP
=>MQ=NP(3)
Xét ΔMBN vuông tại B và ΔPDQ vuông tại D có
BM=DP
BN=DQ
Do đó: ΔMBN=ΔPDQ
=>MN=QP(2)
Xét ΔMAQ vuông tại A và ΔMBN vuông tại B có
MA=MB
AQ=BN
Do đó: ΔMAQ=ΔMBN
=>MQ=MN(1)
Từ (1),(2),(3) suy ra MQ=MN=NP=PQ
=>MNPQ là hình thoi
b: Xét tứ giác BMDP có
BM//DP
BM=DP
Do đó: BMDP là hình bình hành
=>BP//DM
=>KS//GI
Xét tứ giác AQCN có
AQ//CN
AQ=CN
Do đó: AQCN là hình bình hành
=>AN//CQ
=>KI//GS
Xét tứ giác IKSG có
IK//SG
IG//SK
Do đó: IKSG là hình bình hành


1: ta có: AB//CD
mà E\(\in\)AB; F\(\in\)CD
nên AE//DF; BE//CF
2: Ta có: AE+EB=AB
DF+FC=DC
mà AE=DF và AB=DC
nên EB=FC
3: Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
4: Xét tứ giác BEFC có
BE//FC
BE=FC
Do đó BEFC là hình bình hành

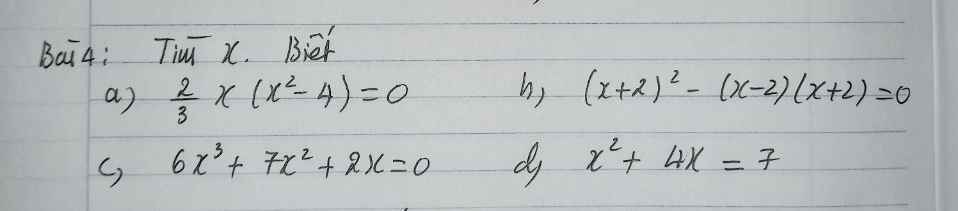
Bài 2:
c: \(C=27x^3-27x^2y+9xy^2-y^3-121\)
\(=\left(3x\right)^3-3\cdot\left(3x\right)^2\cdot y+3\cdot3x\cdot y^2-y^3-121\)
\(=\left(3x-y\right)^3-121=7^3-121=343-121=222\)
Bài 3:
a: \(x^2-4+\left(x-2\right)^2\)
\(=\left(x-2\right)\left(x+2\right)+\left(x-2\right)^2\)
=(x-2)(x+2+x-2)
=2x(x-2)
b: \(x^3-2x^2+x-xy^2\)
\(=x\left(x^2-2x+1-y^2\right)\)
\(=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-1-y\right)\left(x-1+y\right)\)
c: \(x^3-4x^2-12x+27\)
\(=\left(x^3+27\right)-4x\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2-3x+9\right)-4x\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2-7x+9\right)\)
d: \(\left(x^2+x\right)^2-2\left(x^2+x\right)-15\)
\(=\left(x^2+x\right)^2-5\left(x^2+x\right)+3\left(x^2+x\right)-15\)
\(=\left(x^2+x\right)\left(x^2+x-5\right)+3\left(x^2+x-5\right)\)
\(=\left(x^2+x-5\right)\left(x^2+x+3\right)\)