Cho \(a,b,c>0\). Chứng minh rằng
\(\dfrac{ab}{a+b}+\dfrac{bc}{b+c}+\dfrac{ca}{c+a}\le\dfrac{a+b+c}{2}\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt thì và . Bất đẳng thức cần chứng minh trở thành .
Áp dụng bất đẳng thức Cô si cho 3 số dương ta có
hay .
Tương tự, . Cộng theo vế các bất đẳng thức nhận được ta có
Do đó . Đẳng thức xảy ra khi và chỉ khi
.

Đặt thì và do đó áp dụng bất đẳng thức Cô si ta có
.
Đẳng thức xảy ra khi và chỉ khi .


Gọi O, J lần lượt là trung điểm của AB và MB.
Do MB là đường kính của nửa đường tròn tâm J nên ^MIB=90o⇒^CIM=90o.
Vậy nên tứ giác CHMI nội tiếp.
⇒^HIM=^HCM.
Tam giác ACM cân tại C nên ^HCM=^HCA.
Mà ^HCA=^HBC (Cùng phụ góc CAB)
Tam giác IJB cân tại J nên ^HBC=^JIB.
Tóm lại : ^HIM=^JIB⇒^HIM+^MIJ=^JIB+^MIJ
⇒^HIJ=^MIB=90o.
Vậy nên HI là tiếp tuyến tại I của đường trong đường kính MB
Gọi O, J lần lượt là trung điểm của AB và MB.
Do MB là đường kính của nửa đường tròn tâm J nên .
Vậy nên tứ giác CHMI nội tiếp.
.
Tam giác ACM cân tại C nên .
Mà (Cùng phụ góc CAB)
Tam giác IJB cân tại J nên .
suy ra :
Vậy nên HI là tiếp tuyến tại I của đường trong đường kính MB.

Áp dụng bất đẳng thức AM-GM ta có :
\(x+\frac{1}{x-1}=\left[\left(x-1\right)+\frac{1}{x-1}\right]+1\ge2\sqrt{\left(x-1\right)\cdot\frac{1}{x-1}}+1=2+1=3\left(đpcm\right)\)
Đẳng thức xảy ra <=> x = 2

Ta có : a^4 +b^4 +c^4 ≥ a^2b^2 + b^2c^2 + c^2a^2 (*)
Mà a^2b^2+b^2c^2 ≥ 2acb^2
b^2c^2 + c^2a^2 ≥ 2bac^2
c^2a^2+a^2b^2 ≥ bca^2
Cộng theo vế ba bất đẳng thức trên rồi chia hai vế cho 2 ta được
a^2b^2+b^2c^2+ c^2a^2 ≥ abc(a+b+c) (**)
Từ (*)(**) => đpcm

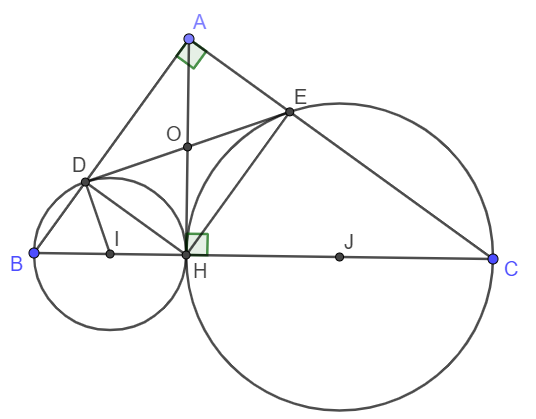
Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chỉ cần chứng minh ID\perp DEID⊥DE .
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC nên ta có: \widehat{BDH}=\widehat{CEH}=90^oBDH=CEH=90o.
Suy ra tứ giác ADHE là hình chữ nhật.
Gọi O là giao điểm của AH và DE, khi đó ta có OD = OH = OE = OA.
Suy ra tam giác ODH cân tại O vì vậy \widehat{ODH}=\widehat{OHD}ODH=OHD.
Ta cũng có tam giác IDH cân tại I suy ra \widehat{IDH}=\widehat{IHO}IDH=IHO.
Suy ra \widehat{IDO}+\widehat{OHD}=\widehat{IHD}+\widehat{IHA}=90^oIDO+OHD=IHD+IHA=90o \Leftrightarrow\widehat{IDO}=90^o⇔IDO=90o hay DI \perp⊥ DE.
Ta có DI\perp DE\left(D\in\left(I\right)\right)DI⊥DE(D∈(I)) suy ra DE tiếp xúc với (I) tại D.
Chứng minh tương tự ta cũng có DE tiếp xúc với (J) tại E.
Vậy DE là tiếp tuyến chung của đường tròn (I) và đường tròn (J).
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC nên ta có : góc BHD = góc CEH=90°
=> tứ giác ADHE là hình chữ nhật
Gọi O là giao điểm của AH và DE khi đó ta có OD=OE=OA
=> Tam giác ODH cân tại O vì vậy góc ODH = góc OHD
Ta cũng có tam giác IDH cân tại I suy ra góc IDH= góc IHO
=> góc IDO + góc OHD = góc IHD + góc IHA=90° <=> góc IDO = 90° hay DI ⊥ DE
ta có DI ⊥ DE ( D ∈ I) => DE tiếp xúc với (I) tại D
Ta có DE tiếp xúc với (J) tại E
Vậy DE là tiếp tuyến chung của đường tròn (I) và đường tròn (J)

Sử dụng bất đẳng thức Cô si ta có
\sqrt{ab}+3\sqrt{bc}+5\sqrt{ca}\le\dfrac{a+b}{2}+3.\dfrac{b+c}{2}+5.\dfrac{c+a}{2}ab+3bc+5ca≤2a+b+3.2b+c+5.2c+a
=3a+2b+4c=3a+2b+4c
Từ đó 3a+2b+4c\ge\sqrt{ab}+3\sqrt{bc}+5\sqrt{ca}3a+2b+4c≥ab+3bc+5ca.
Áp dụng bất đẳng thức Cô si ta được
\(\sqrt{ab}+3\sqrt{bc}+5\sqrt{ac}\) ≤ a+b/2 + 3/2*(b+c) + 5/2*(a+c) = 3a +2b+4c
<=> đpcm

Áp dụng bất đẳng thức cô si ta có, với a,b,c >0
a/bc + b/ac ≥ 2*1/c
b/ac + c/ab ≥ 2*1/a
a/bc + c/ab ≥ 2*1/b
Cộng từng vế của 3 bất đẳng thức trên với nhau ta được
2*(a/bc + b/ac + c/ab) ≥ 2(1/a+1/b+1/c)
<=> đpcm
Sử dụng bất đẳng thức Cô si cho hai số dương ta có:
Viết hai bất đẳng thức tương tự rồi cộng theo vế ba bất đẳng thức nhận được rồi chia 2 vế bất đẳng thức cho 2 ta được đpcm.
Áp dụng bất đẳng thức AM-GM ta có :
\(ab\le\frac{\left(a+b\right)^2}{4}\)=> \(\frac{ab}{a+b}\le\frac{a+b}{4}\)
Tương tự : \(\frac{bc}{b+c}\le\frac{b+c}{4}\); \(\frac{ca}{c+a}\le\frac{c+a}{4}\)
Cộng vế với vế các bđt trên ta có đpcm
Đẳng thức xảy ra <=> a=b=c
Có ab\le\dfrac{\left(a+b\right)^2}{4}\Rightarrow\dfrac{ab}{a+b}\le\dfrac{a+b}{4}ab≤4(a+b)2⇒a+bab≤4a+b.