Tính nhanh:
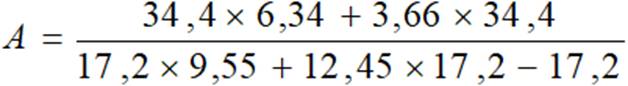
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Khi kéo dài BC về phía B thêm 5cm thì diện tích tăng thêm 37,5cm2 nên 5 lần chiều cao của tam giác NBC là:
2x37,5=75(cm)
=>Chiều cao của tam giác NCB là 75:5=15(cm)
Độ dài đoạn BC là:
150x2:15=300:15=20(cm)

Lời giải:
$118,24-(2:5+x\times 3)=27,12\times 2$
$118,24-(0,4+x\times 3)=54,24$
$0,4+x\times 3=118,24-54,24=64$
$x\times 3=64-0,4=63,6$
$x=63,6:3=21,2$

Lời giải:
$7,5\times x+2,45\times x=20$
$x\times (7,5+2,45)=20$
$x\times 9,95=20$
$x=20:9,95=2,01$

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{ABE}\) là góc tạo bởi tiếp tuyến BA và dây cung BE
\(\widehat{BFE}\) là góc nội tiếp chắn cung BE
Do đó: \(\widehat{ABE}=\widehat{BFE}\)
Xét ΔABE và ΔAFB có
\(\widehat{ABE}=\widehat{AFB}\)
\(\widehat{BAE}\) chung
Do đó: ΔABE~ΔAFB
=>\(\dfrac{AB}{AF}=\dfrac{AE}{AB}\)
=>\(AB^2=AF\cdot AE\)
c: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại X
ΔOEF cân tại O
mà OD là đường trung tuyến
nên OD\(\perp\)FE tại D
Xét ΔAXK vuông tại X và ΔADO vuông tại D có
\(\widehat{XAK}\) chung
Do đó: ΔAXK~ΔADO
=>\(\dfrac{AX}{AD}=\dfrac{AK}{AO}\)
=>\(AX\cdot AO=AD\cdot AK\)
Xét ΔABO vuông tại B có BX là đường cao
nên \(AX\cdot AO=AB^2\)
=>\(AE\cdot AF=AK\cdot AD\)
Ta có: \(\widehat{ADO}=\widehat{ABO}=\widehat{ACO}=90^0\)
=>A,D,B,C,O cùng thuộc đường tròn đường kính AO

Đây là toán nâng cao của nâng cao chuyên đề dãy số cách đều, cấu trúc
Giải:
Cứ 3 lon bia đổi được 1 lon bia nên số lon bia mất đi sau mỗi lần đổi là:
3 - 1 = 2 (lon bia)
Sau lần đổi thứ nhất số lon bia còn lại là: 30 - 2 = 28 (lon)
Sau lần đổi cuối cùng số lon bia còn lại là 2 lon (vì 2 < 3 nên không thể đổi được nữa)
Số lần đổi vỏ lon bia là: (28 - 2) : 2 + 1 = 14 (lần)
Vậy tổng số lon bia mà ngườ đó có thể uống được khi mua 30 lon bia và được tặng là:
3 x 14 + 2 = 44 (lon bia)
Đáp số: 44 lon bia

b: Phương trình hoành độ giao điểm là:
\(x^2=x+2\)
=>\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Khi x=2 thì \(y=2^2=4\)
Khi x=-1 thì \(y=\left(-1\right)^2=1\)
Vậy: A(-1;1); B(2;4)
C thuộc (P)
=>\(C\left(x;x^2\right)\)
B(2;4); A(-1;1); C(x;x2)
\(\overrightarrow{BA}=\left(-3;-3\right);\overrightarrow{BC}=\left(x-2;x^2-4\right)\)
ΔBAC vuông tại B
=>\(\overrightarrow{BA}\cdot\overrightarrow{BC}=0\)
=>\(-3\left(x-2\right)+\left(-3\right)\left(x^2-4\right)=0\)
=>\(\left(x-2\right)+\left(x^2-4\right)=0\)
=>\(x^2+x-6=0\)
=>(x+3)(x-2)=0
=>\(\left[{}\begin{matrix}x=-3\left(nhận\right)\\x=2\left(loại\right)\end{matrix}\right.\)
Khi x=-3 thì \(y=\left(-3\right)^2=9\)
vậy: C(-3;9); A(-1;1); B(2;4)
\(BA=\sqrt{\left(-1-2\right)^2+\left(1-4\right)^2}=3\sqrt{2}\)
\(BC=\sqrt{\left(-3-2\right)^2+\left(9-4\right)^2}=5\sqrt{2}\)
\(AC=\sqrt{\left(-3+1\right)^2+\left(9-1\right)^2}=2\sqrt{17}\)
Khoảng cách từ B đến AC là:
\(\dfrac{BA\cdot BC}{AC}=\dfrac{3\sqrt{2}\cdot5\sqrt{2}}{2\sqrt{17}}=\dfrac{15}{\sqrt{17}}\)
\(A=\dfrac{34,4\text{x}6,34+3,66\text{x}34,4}{17,2\text{x}9,55+12,45\text{x}17,2-17,2}\)
\(=\dfrac{34,6\text{x}\left(6,34+3,66\right)}{17,2\text{x}\left(9,55+12,45-1\right)}\)
\(=\dfrac{34,6\text{x}10}{17,2\text{x}21}=\dfrac{865}{903}\)