Mình cần giải câu này ạ. Cho a nguyên, tìm (2a+3;3a+4)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA⊥BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\)

a: Xét tứ giác AEDB có \(\hat{AEB}=\hat{ADB}=90^0\)
nên AEDB là tứ giác nội tiếp
b: Ta có: AD⊥BC
OM⊥BC
Do đó: AD//OM
=>\(\hat{BAD}=\hat{BPM}\) (hai góc đồng vị)
mà \(\hat{BAD}=\hat{BED}\) (AEDB nội tiếp)
nên \(\hat{BED}=\hat{BPM}\)

- \(M\) và \(K\) là các trung điểm của các cạnh \(B C\) và \(A D\) của tứ giác \(A B C D\), do đó, ta có:
\(B M = M C \text{v} \overset{ˋ}{\text{a}} A K = K D\) - \(A M\) và \(B K\) cắt nhau tại \(H\).
- \(D M\) và \(C K\) cắt nhau tại \(L\).
Ta biết rằng diện tích của một tam giác có thể tính theo công thức:
\(S = \frac{1}{2} \times độ\&\text{nbsp};\text{d} \overset{ˋ}{\text{a}} \text{i}\&\text{nbsp};đ \overset{ˊ}{\text{a}} \text{y} \times \text{chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{cao} .\)
Khi các đường chéo cắt nhau, ta có thể tính diện tích của các tam giác con trong tứ giác thông qua các đoạn thẳng cắt nhau.
Diện tích của các tam giác trong tứ giác:
- Diện tích của tam giác \(A B H\) là:
\(S_{A B H} = \frac{1}{2} \times A B \times h_{A B H} ,\)
trong đó \(h_{A B H}\) là chiều cao từ \(H\) xuống đáy \(A B\). - Diện tích của tam giác \(C D L\) là:
\(S_{C D L} = \frac{1}{2} \times C D \times h_{C D L} ,\)
trong đó \(h_{C D L}\) là chiều cao từ \(L\) xuống đáy \(C D\).
Tổng diện tích của tứ giác \(H K L M\) có thể được chia thành diện tích của các tam giác nhỏ:
\(S_{H K L M} = S_{A B H} + S_{C D L} .\)Do đó, ta đã chứng minh rằng diện tích của tứ giác \(H K L M\) bằng tổng diện tích của hai tam giác \(A B H\) và \(C D L\), như yêu cầu.
Kết luận:
Diện tích tứ giác \(H K L M\) bằng tổng diện tích của hai tam giác \(A B H\) và \(C D L\).

\(x+y\) = 4
\(x=4-y\)
Thay \(4-y\) vào biểu thức \(xy=1\)
Ta có: (4 - y).y = 1
4y - \(y^2\) = 1
-(y\(^2\) - 4y + 4) = - 3
(y - 2)\(^2\) = 3
\(\left[\begin{array}{l}y-2=\sqrt3\\ y-2=-\sqrt3\end{array}\right.\)
\(\left[\begin{array}{l}y=\sqrt3+2\\ y=-\sqrt3+2\end{array}\right.\)
\(\left[\begin{array}{l}x=4-\sqrt3-2\\ x=4+\sqrt3-2\end{array}\right.\)
\(\left[\begin{array}{l}x=\left(4-2\right)-\sqrt3\\ x=\left(4-2\right)+\sqrt3\end{array}\right.\)
\(\left[\begin{array}{l}x=2-\sqrt3\\ x=2+\sqrt3\end{array}\right.\)
Vậy: ...

a: Xét tứ giác OBAC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên OBAC là tứ giác nội tiếp
b: Xét (O) có
AB,AC là các tiếp tuyến
DO đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=R^2\)

1: Khi x=25 thì \(A=\frac{5-1}{5+3}=\frac28=\frac14\)
2: \(B=\frac{x+2}{\sqrt{x}-1}-\frac{3}{\sqrt{x}+1}-\frac{x-\sqrt{x}+4}{x-1}\)
\(=\frac{\left(x+2\right)\left(\sqrt{x}+1\right)-3\left(\sqrt{x}-1\right)-x+\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\frac{x\sqrt{x}+x+2\sqrt{x}+2-3\sqrt{x}+3-x+\sqrt{x}-4}{x-1}=\frac{x\sqrt{x}+1}{x-1}=\frac{x-\sqrt{x}+1}{\sqrt{x}-1}\)
3:
A>0
=>\(\frac{\sqrt{x}-1}{\sqrt{x}+3}>0\)
=>\(\sqrt{x}-1>0\)
=>x>1
\(B-3=\frac{x-\sqrt{x}+1-3\left(\sqrt{x}-1\right)}{\sqrt{x}-1}=\frac{x-4\sqrt{x}+4}{\sqrt{x}-1}=\frac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}\)
mà x>1
nên B-3>0
=>B>3
1: Khi x=25 thì \(A=\frac{5-1}{5+3}=\frac28=\frac14\)
2: \(B=\frac{x+2}{\sqrt{x}-1}-\frac{3}{\sqrt{x}+1}-\frac{x-\sqrt{x}+4}{x-1}\)
\(=\frac{\left(x+2\right)\left(\sqrt{x}+1\right)-3\left(\sqrt{x}-1\right)-x+\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\frac{x\sqrt{x}+x+2\sqrt{x}+2-3\sqrt{x}+3-x+\sqrt{x}-4}{x-1}=\frac{x\sqrt{x}+1}{x-1}=\frac{x-\sqrt{x}+1}{\sqrt{x}-1}\)
3:
A>0
=>\(\frac{\sqrt{x}-1}{\sqrt{x}+3}>0\)
=>\(\sqrt{x}-1>0\)
=>x>1
\(B-3=\frac{x-\sqrt{x}+1-3\left(\sqrt{x}-1\right)}{\sqrt{x}-1}=\frac{x-4\sqrt{x}+4}{\sqrt{x}-1}=\frac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}\)
mà x>1
nên B-3>0
=>B>3

Giải:
Số học sinh của nhóm là:
4 + 5 + 4 + 3 + 3 + 1 = 20 (học sinh)
Tần số tương đối của giá trị dưới điểm 7 là:
\(\frac{4+5}{30}\) x 100% = 30%
Vậy nhóm đó có 20 học sinh, và tần số tương đối của giá trị dưới 7 điểm là: 30%
Câu 2:
Các số là bội của 5 hoặc 9 từ 1 đến 20 là các số thuộc dãy số:
5; 9; 10; 15; 18; 20
Có 6 kết quả thuận lợi cho biến cố A
Xác suất của biến cố A: "số ghi trên thẻ lấy được là bội của 5 hoặc 9" là:
6 : 20 = \(\frac{3}{10}\)

a: Sửa đề: \(S=\dfrac{1}{\sqrt{1}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{9}}+...+\dfrac{1}{\sqrt{4n-3}+\sqrt{4n+1}}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}}{4}+\dfrac{-\sqrt{5}+\sqrt{9}}{4}+...+\dfrac{-\sqrt[]{4n-3}+\sqrt{4n+1}}{4}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}-\sqrt{5}+\sqrt{9}-...-\sqrt{4n-3}+\sqrt{4n+1}}{4}=\dfrac{\sqrt{4n+1}-1}{4}\)
b: \(T=\dfrac{\sqrt{2-\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{5-\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\dfrac{\sqrt{4-2\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{10-2\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{1-\sqrt{3}}-\dfrac{\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{3}-1}{1-\sqrt[]{3}}-\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(-1+\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{7}-\sqrt{3}}\right)=0\)

\(\text{Δ}=5^2-4\left(m-3\right)=25-4m+12=-4m+37\)
Để phương trình có hai nghiệm thì Δ>=0
=>-4m+37>=0
=>-4m>=-37
=>\(m< =\dfrac{37}{4}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-5\\x_1x_2=\dfrac{c}{a}=m-3\end{matrix}\right.\)
\(2x_1x_2-\left(x_1+x_2\right)=2\)
=>\(2\left(m-3\right)-\left(-5\right)=2\)
=>2m-6+5=2
=>2m-1=2
=>2m=3
=>\(m=\dfrac{3}{2}\left(nhận\right)\)



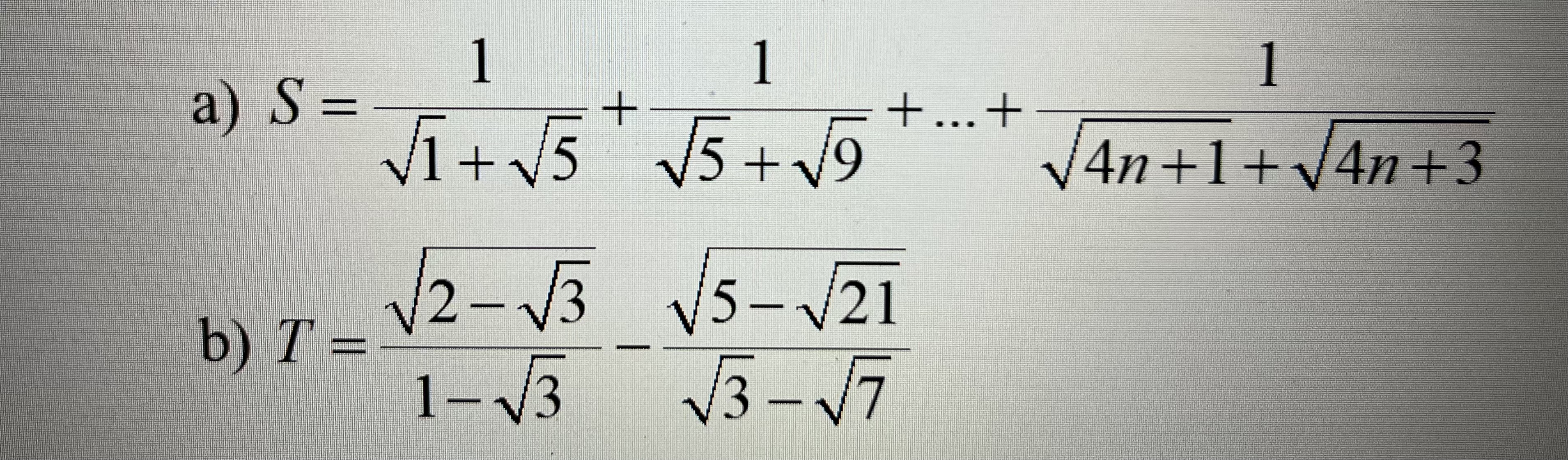
Gọi d = ƯCLN(2a + 3; 3a + 4)
⇒ (2a + 3) ⋮ d và (3a + 4) ⋮ d
*) (2a + 3) ⋮ d
⇒ 3(2a + 3) ⋮ d
⇒ (6a + 9) ⋮ d (1)
*) (3a + 4) ⋮ d
⇒ 2(3a + 4) ⋮ d
⇒ (6a + 8) ⋮ d (2)
Từ (1) và (2) suy ra:
⇒ [(6a + 9) - (6a + 8)] ⋮ d
⇒ (6a + 9 - 6a - 8) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy ƯCLN(2a + 3; 3a + 4) = 1
cs phải tìm ƯCLN ko bn