Tia đối của mỗi tia Ox, Oy, Oz là phân giác của góc hợp bởi hai tia còn lại
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-45^0}{2}=67,5^0\)
Xét ΔABC có \(\widehat{ABC}=\widehat{ACB}>\widehat{BAC}\)
mà AC,AB,BC lần lượt là cạnh đối diện của các góc ABC,ACB,BAC
nên AC=AB>BC
b: Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
=>\(\widehat{BDC}=\widehat{CEB}\)
c: D nằm trên đường trung trực của AC
=>DA=DC
Xét ΔDAC có DA=DC và \(\widehat{DAC}=45^0\)
nên ΔDAC vuông cân tại D
=>\(\widehat{ADC}=90^0\)
=>CD\(\perp\)AB
=>\(\widehat{CDB}=\widehat{CEB}=90^0\)
=>BE\(\perp\)AC
ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
Xét ΔABC có
AM,BE,CD là các đường cao
Do đó: AM,BE,CD đồng quy

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
HA chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
b: Xét ΔBHA vuông tại H và ΔBHD vuông tại H có
BH chung
HA=HD
Do đó: ΔBHA=ΔBHD
=>BA=BD
=>ΔBAD cân tại B
c: Ta có: \(\widehat{BDA}=\widehat{BAD}\)(ΔBAD cân tại B)
\(\widehat{BAD}=\widehat{CAH}\)(cmt)
Do đó: \(\widehat{BDA}=\widehat{DAC}\)
=>BD//AC

Gọi A là biến cố "Số ghi trên thẻ là số chia 6 dư 2"
=>A={2;8;14;20;26}
=>n(A)=5
\(P_A=\dfrac{5}{30}=\dfrac{1}{6}\)

1; (\(\dfrac{3}{4}\))2. 42 - (\(\dfrac{1}{2}\))2 : 2 - 2\(\dfrac{3}{4}\)
= \(\dfrac{3^2}{4^2}\).42 - \(\dfrac{1}{4}\) : 2 - 2\(\dfrac{3}{4}\)
= 9 - \(\dfrac{1}{8}\) - \(\dfrac{11}{4}\)
= \(\dfrac{72}{8}\) - \(\dfrac{1}{8}-\dfrac{22}{8}\)
= \(\dfrac{71}{8}\) - \(\dfrac{22}{8}\)
= \(\dfrac{49}{8}\)
2; (\(\dfrac{3}{5}\))2.52 - (2\(\dfrac{1}{4}\))3 : (\(\dfrac{3}{4}\))3 - 3
= \(\dfrac{9}{5^2}\).52 - (\(\dfrac{9}{4}\))3 : (\(\dfrac{3}{4}\))3 - 3
= 9 - (\(\dfrac{9}{4}\) : \(\dfrac{3}{4}\))3 - 3
= 9 - 33 - 3
= 9 - 27 - 3
= 9 - (27 + 3)
= 9 - 30
= - 21

a: ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔAMO vuông tại M và ΔANO vuông tại N có
AO chung
AM=AN
Do đó: ΔAMO=ΔANO
b: O nằm trên đường trung trực của AB
=>OA=OB
O nằm trên đường trung trực của AC
=>OA=OC
Do đó: OA=OB=OC
c: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
=>\(\widehat{BAO}=\widehat{CAO}\)
=>AO là phân giác của góc BAC
d: Ta có: \(\widehat{IBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ICB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
=>I nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,I thẳng hàng

a: Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
=>\(GB=\dfrac{2}{3}BM;CG=\dfrac{2}{3}CN\)
mà BM=CN
nên GB=GC
b: Sửa đề: Chứng minh ΔBGN=ΔCOM
Ta có: GB+GM=BM
GC+GN=CN
mà BM=CN và GB=GC
nên GM=GN
Xét ΔGNB và ΔGMC có
GN=GM
\(\widehat{NGB}=\widehat{MGC}\)(hai góc đối đỉnh)
GB=GC
Do đó: ΔGNB=ΔGMC
c: ΔGNB=ΔGMC
=>NB=MC
mà \(NB=\dfrac{AB}{2};MC=\dfrac{AC}{2}\)
nên AB=AC
=>ΔABC cân tại A
d: Xét ΔABC có
AI,BM,CN là các đường trung tuyến
Do đó: AI,BM,CN đồng quy
vẽ hộ em bài này
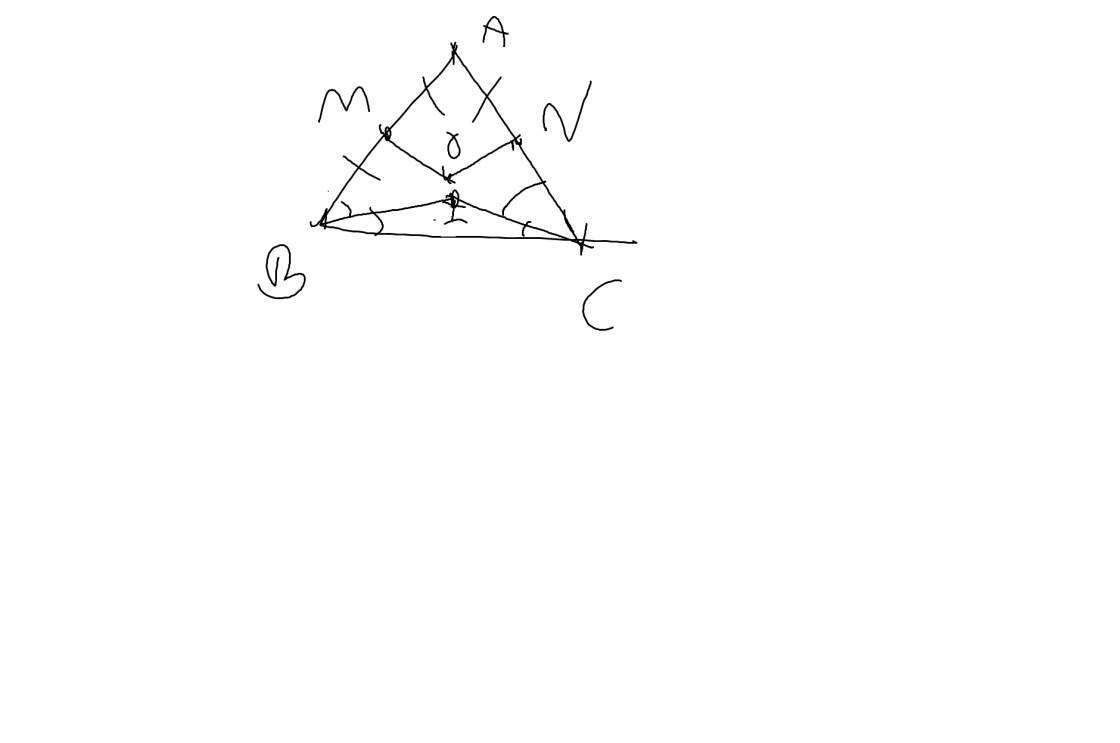
4. (1,5 điểm) Cho ABC có hai đường trung tuyến BM và CN bằng nhau và cắt nhau tai G. a) Chứng minh GB = GC. b) Chứng minh BON = COM c) Chứng minh ABC cân, chỉ rõ cân tại đâu. d) Gọi I là trung điểm BC. Chứng minh AI, BM, CN đồng quy.

1: \(\dfrac{1}{2}-\left(\dfrac{2}{3}\right)^9:\left(\dfrac{2}{3}\right)^7+\dfrac{5}{6}\)
\(=\dfrac{1}{2}-\left(\dfrac{2}{3}\right)^2+\dfrac{5}{6}\)
\(=\dfrac{1}{2}-\dfrac{4}{9}+\dfrac{5}{6}\)
\(=\dfrac{9}{18}-\dfrac{8}{18}+\dfrac{15}{18}=\dfrac{16}{18}=\dfrac{8}{9}\)
2: \(\left(\dfrac{3}{7}\right)^3\cdot\left(\dfrac{7}{6}\right)^3+\dfrac{2}{3}:\left(\dfrac{4}{3}\right)^2\)
\(=\dfrac{1}{8}+\dfrac{2}{3}:\dfrac{16}{9}\)
\(=\dfrac{1}{8}+\dfrac{2}{3}\cdot\dfrac{9}{16}\)
\(=\dfrac{1}{8}+\dfrac{3}{8}=\dfrac{4}{8}=\dfrac{1}{2}\)
3: \(-\dfrac{4}{7}:\dfrac{9}{14}+\left(\dfrac{4}{3}\right)^4:\left(\dfrac{4}{3}\right)^2\)
\(=-\dfrac{4}{7}\cdot\dfrac{14}{9}+\left(\dfrac{4}{3}\right)^2\)
\(=-\dfrac{8}{9}+\dfrac{16}{9}=\dfrac{8}{9}\)
4: \(\left(-\dfrac{4}{3}+1\right)-\left(-\dfrac{2}{3}\right)^{21}:\left(-\dfrac{2}{3}\right)^{19}\)
\(=\dfrac{-1}{3}-\left(-\dfrac{2}{3}\right)^2\)
\(=-\dfrac{1}{3}-\dfrac{4}{9}=-\dfrac{7}{9}\)
5: \(\left(\dfrac{5}{2}-\dfrac{4}{3}\right)\cdot\dfrac{6}{7}+\left(-\dfrac{3}{2}\right)^5:\left(-\dfrac{3}{2}\right)^3\)
\(=\dfrac{15-8}{6}\cdot\dfrac{6}{7}+\left(-\dfrac{3}{2}\right)^2\)
\(=1+\dfrac{9}{4}=\dfrac{13}{4}\)
6: \(25^{10}\cdot\left(\dfrac{1}{5}\right)^{20}+\left(-\dfrac{3}{4}\right)^8\cdot\left(-\dfrac{4}{3}\right)^8-2011^0\)
\(=\dfrac{5^{20}}{5^{20}}+1-1=1+1-1=1\)
7: \(\left(\dfrac{3}{5}\right)^{10}\cdot\left(\dfrac{5}{3}\right)^{10}-\dfrac{13^4}{39^4}+2014^0\)
\(=\left(\dfrac{3}{5}\cdot\dfrac{5}{3}\right)^{10}-\dfrac{1}{3^4}+1\)
\(=1+1-\dfrac{1}{81}=2-\dfrac{1}{81}=\dfrac{161}{81}\)
8: \(\left(-0,5\right)^5:\left(-0,5\right)^3-\left(\dfrac{17}{2}\right)^7:\left(\dfrac{17}{2}\right)^6\)
\(=\left(-0,5\right)^2-\dfrac{17}{2}\)
\(=\dfrac{1}{4}-\dfrac{17}{2}=\dfrac{1}{4}-\dfrac{34}{4}=-\dfrac{33}{4}\)

a: ta có: \(\widehat{ABD}=\widehat{CBD}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\widehat{BCE}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{CBD}=\widehat{ACE}=\widehat{BCE}\)
Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
=>OB=OC

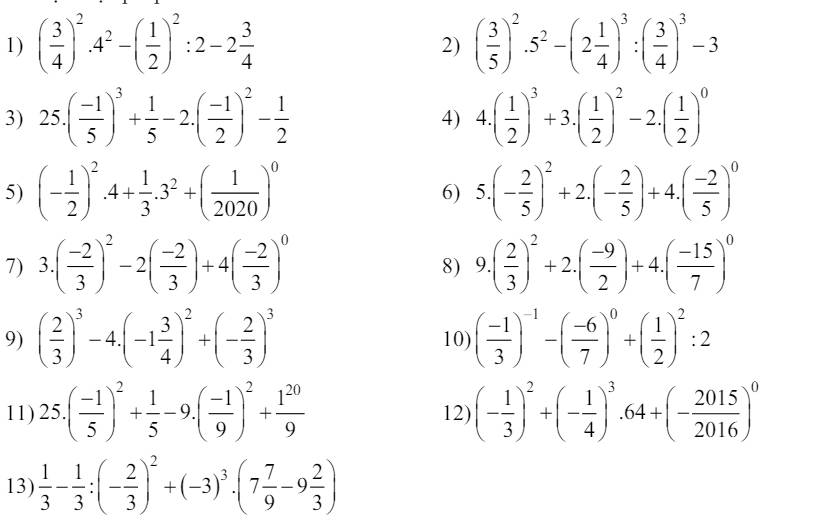
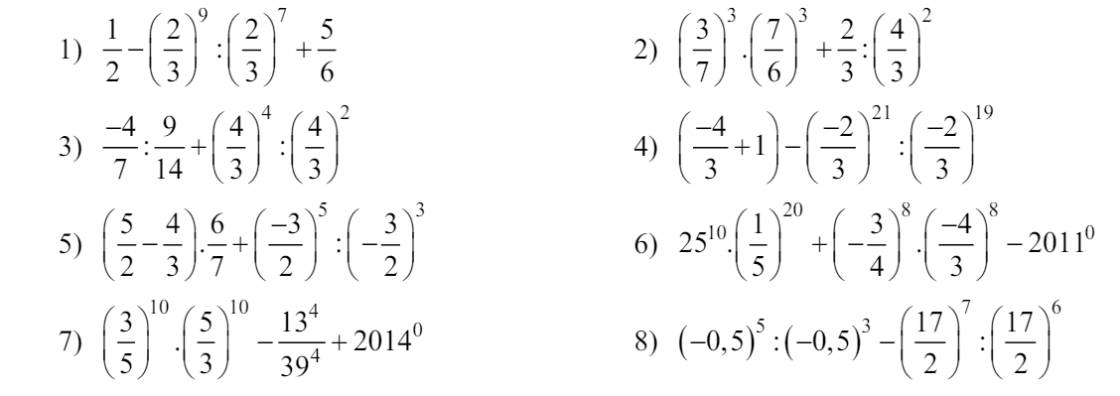

Rồi sau đó em cần làm gì với dữ liệu này?