
 mọi người ơi giúp em vớiiii
mọi người ơi giúp em vớiiii
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


sửa đề chia hết 31 nhé
\(S=5+5^2+5^3+...+5^{2019}=5\left(1+5+5^2+5^3\right)+...+5^{2016}\left(1+5+5^2+5^3\right)\)
\(=31\left(5+...+5^{2016}\right)⋮31\)
Vậy ta có đpcm

Bài 2:
a) \(\dfrac{-7}{-13}=\dfrac{7}{13}\) là số hưu tỉ dương
b) \(\dfrac{2}{-17}=-\dfrac{2}{17}\) là số hưu tỉ âm
c) \(-\dfrac{-6}{5}=\dfrac{6}{5}\) là số hưu tỉ dương
Bài 3:
a) \(-2\dfrac{1}{4}=-\left(2+\dfrac{1}{4}\right)=-\dfrac{9}{4}\)
b) \(6\dfrac{2}{3}=6+\dfrac{2}{3}=\dfrac{20}{3}\)
c) \(-3\dfrac{1}{4}=-\left(3+\dfrac{1}{4}\right)=-\dfrac{13}{4}\)

Bài 6:
\(\dfrac{9^5.9^7}{3^{22}}\) = \(\dfrac{3^{15}.3^{21}}{3^{22}}\) = \(\dfrac{3^{36}}{3^{22}}\) = 314
Bài 7:
\(\dfrac{9^{16}.8^{11}}{6^{33}}\) = \(\dfrac{3^{32}.2^{33}}{3^{33}.2^{33}}\) = \(\dfrac{1}{3}\)

\(N=-1-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{10}}\right)\)
Xét \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{10}}\)
\(\dfrac{1}{2}A=\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{11}}\Rightarrow\dfrac{1}{2}A-A=\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{11}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{10}}\right)\)
\(\Leftrightarrow-\dfrac{1}{2}A=-\dfrac{1}{2}+\dfrac{1}{2^{11}}\Rightarrow A=-\dfrac{1}{2^{10}}\)
\(\Rightarrow N=-1-\left(-\dfrac{1}{2^{10}}\right)=-1+\dfrac{1}{2^{10}}\)
=> Vậy ko tm đpcm

\(\dfrac{x}{2}+\dfrac{x}{3}-1=\dfrac{1}{6}\Rightarrow3x+2x-6=1\Leftrightarrow5x=7\Leftrightarrow x=\dfrac{7}{5}\)

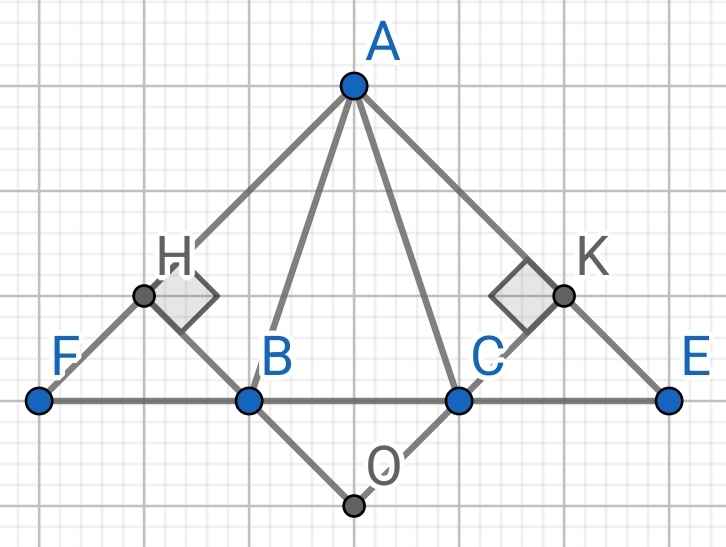
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC và ∠ABC = ∠ACB
Ta có:
∠ABF + ∠ABC = 180⁰ (kề bù)
∠ACE + ∠ACB = 180⁰ (kề bù)
Mà ∠ABC = ∠ACB (cmt)
⇒ ∠ABF = ∠ACE
Xét ∆ABF và ∆ACE có:
AB = AC (cmt)
∠ABE = ∠ACF (cmt)
BF = CE (gt)
⇒ ∆ABF = ∆ACE (c-g-c)
⇒ AF = AE (hai cạnh tương ứng)
⇒ ∆AEF cân tại A
b) *) Cách 1:
Do ∆ABF = ∆ACE (cmt)
⇒ ∠BAF = ∠CAE (hai góc tương ứng)
⇒ ∠BAH = ∠CAK
Xét hai tam giác vuông: ∆ABH và ∆ACK có:
AB = AC (cmt)
∠BAH = ∠CAK (cmt)
⇒ ∆ABH = ∆ACK (cạnh huyền - góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
*) Cách 2:
Do ∆AEF cân tại A (cmt)
⇒ ∠AFE = ∠AEF
⇒ ∠HFB = ∠KEC
Xét hai tam giác vuông: ∆BHF và ∆CKE có:
BF = CE (gt)
∠HFB = ∠KEC (cmt)
⇒ ∆BHF = ∆CKE (cạnh huyền - góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
c) Sửa đề: Gọi O là giao điểm của HB và KC
Do ∆BHF = ∆CKE (cmt)
⇒ ∠HBF = ∠KCE (hai góc tương ứng)
Mà ∠CBO = ∠HBF (đối đỉnh)
∠BCO = ∠KCE (đối đỉnh)
⇒ ∠CBO = ∠BCO
⇒ ∆BOC cân tại O

Sửa đề: \(B=\left(1+\dfrac{1}{1\cdot3}\right)\cdot\left(1+\dfrac{1}{2\cdot4}\right)\cdot...\cdot\left(1+\dfrac{1}{2022\cdot2024}\right)\)
\(=\left(1+\dfrac{1}{2^2-1}\right)\cdot\left(1+\dfrac{1}{3^2-1}\right)\cdot...\cdot\left(1+\dfrac{1}{2023^2-1}\right)\)
\(=\dfrac{2^2}{2^2-1}\cdot\dfrac{3^2}{3^2-1}\cdot...\cdot\dfrac{2023^2}{2023^2-1}\)
\(=\dfrac{2\cdot3\cdot...\cdot2023}{1\cdot2\cdot...\cdot2022}\cdot\dfrac{2\cdot3\cdot....\cdot2023}{3\cdot4\cdot...\cdot2024}\)
\(=\dfrac{2023}{1}\cdot\dfrac{2}{2024}=\dfrac{2023}{1012}\)

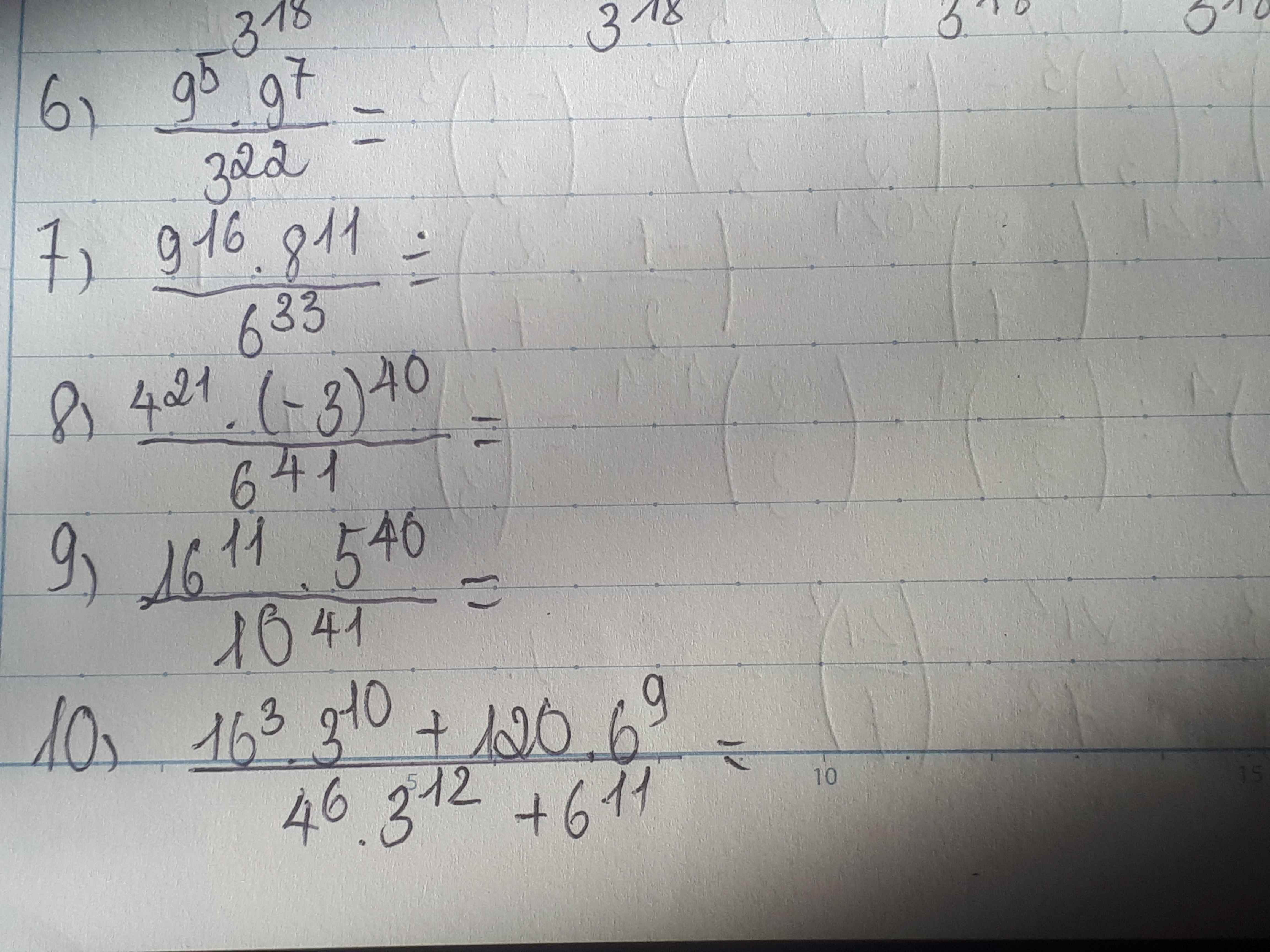

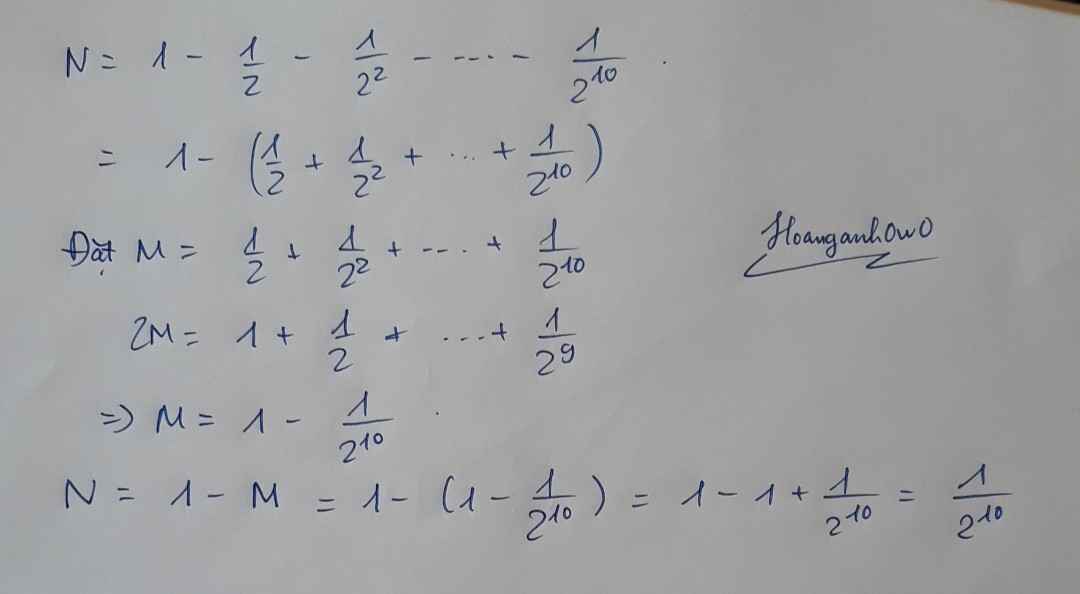
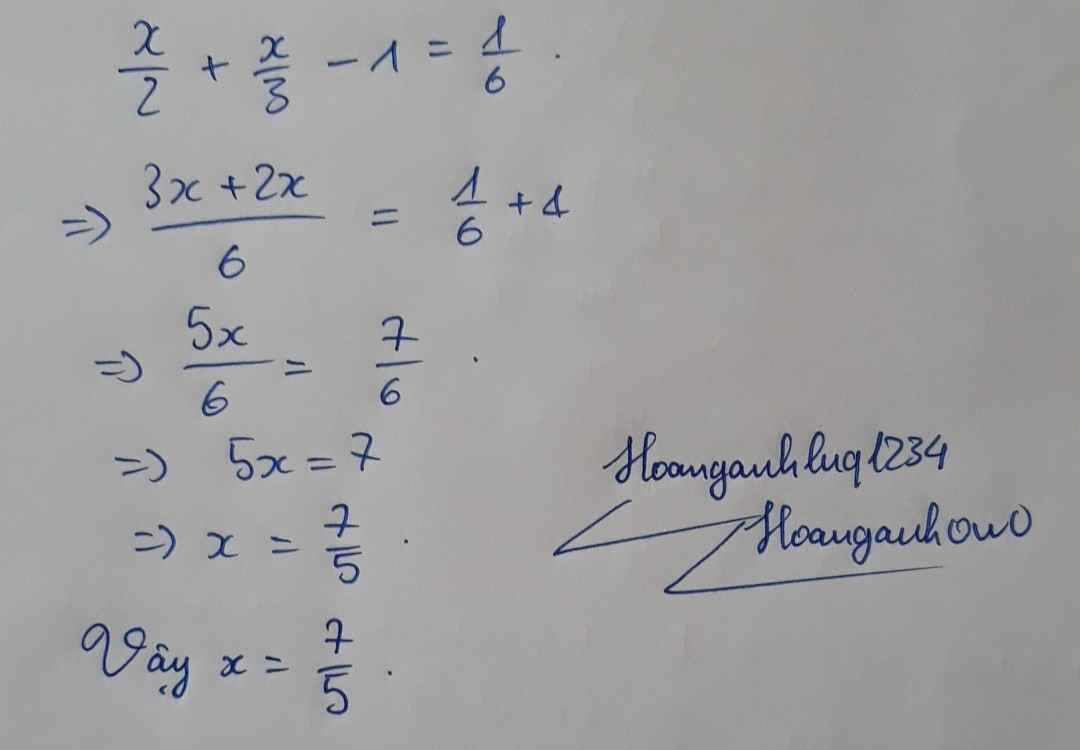
Bài 6: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{142^0}{2}=71^0\)
Ta có: \(\widehat{xOz}+\widehat{x'Oz}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Oz}+71^0=180^0\)
=>\(\widehat{x'Oz}=109^0\)
Bài 7:
Ta có: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{180^0}{2}=90^0\)
Ot là phân giác của góc xOz
=>\(\widehat{zOt}=\dfrac{\widehat{xOz}}{2}=\dfrac{90^0}{2}=45^0\)
Ov là phân giác của góc yOz
=>\(\widehat{vOz}=\dfrac{90^0}{2}=45^0\)
\(\widehat{vOt}=\widehat{zOv}+\widehat{zOt}=45^0+45^0=90^0\)