Diện tích tấm bìa ban đầu là:

\(\frac95\times\frac56=\frac32(m^2)\)

Diện tích tấm bìa Hoa đã cắt đi là:

\(\frac32\times\frac45=\frac65(m^2)\)

Diện tích tấm bìa còn lại là:

\(\frac32-\frac65=\frac{3}{10}(m^2)\)

Diện tích của tấm bìa đó là:

     \(\dfrac{9}{5}\times\dfrac{5}{6}=\dfrac{3}{2}=1,5\) ( m² )

Hoa đã cắt số mét vuông là:

     1,5 x \(\dfrac{4}{5}\) = 1,2 ( m² )

Diện tích còn lại của tấm bìa là:

     1,5 - 1,2 = 0,3 ( m² )

           Đáp số: 0,3 m²

a)Sau 2 năm , xã đó tăng số người là :

60+40=100(người)

b)Sau năm 2023 , xã đó có số người là :

5038+40+60=5138(người)

Đáp số : a)100 người

              b)5138 người

a) Đến năm 2022, xã đó có số người là:

5038 + 40 = 5078 (người)

Sau 2 năm xã đó tăng số người là:

40 + 60 = 100 (người)

b) Sau năm 2023, xã đó có số người là:

5078 + 60 = 5138 ( người)

Đ/s:

a: \(\dfrac{1}{2}< \dfrac{12}{a}< \dfrac{4}{3}\)

=>\(\dfrac{12}{24}< \dfrac{12}{a}< \dfrac{12}{9}\)

=>9<a<24

mà a nguyên

nên \(a\in\left\{10;11;...;23\right\}\)

b: \(\dfrac{7}{4}< \dfrac{a}{8}< 3\)

=>\(\dfrac{14}{8}< \dfrac{a}{8}< \dfrac{24}{8}\)

=>14<a<24

mà a nguyên

nên \(a\in\left\{15;16;...;23\right\}\)

c: \(\dfrac{2}{3}< \dfrac{a-1}{6}< \dfrac{8}{9}\)

=>\(\dfrac{12}{18}< \dfrac{3\left(a-1\right)}{18}< \dfrac{16}{18}\)

=>12<3a-3<16

=>15<3a<19

=>5<a<19/3

mà a nguyên

nên a=6

d: \(\dfrac{12}{9}< \dfrac{4}{a}< \dfrac{8}{3}\)

=>\(\dfrac{8}{6}< \dfrac{8}{2a}< \dfrac{8}{3}\)

=>3<2a<6

mà a nguyên

nên 2a=4

=>a=2

Giải:

Chiều rộng của thửa ruộng hình chữ nhật đó là:

     320 x \(\dfrac{3}{8}\) = 120 ( m )

Diện tích thửa ruộng hình chữ nhật đó là:

     320 x 120 = 38400 ( m² )

Trên cả thửa ruộng đó người ta thu hoạch được số ki-lô-gam thóc là:

     70 x ( 38400 : 100 ) = 26880 ( kg )

               Đáp số: 26880 kg thóc

Chiều rộng thửa ruộng đó là :

320x3/8=120(m)

Diện tích thửa ruộng đó là :

320x120=38400(m²)

Trên cả thửa ruộng đó người ta thu hoạch được số ki-lô-gam thóc là:

38400:100x70=26880(kg)

Đáp số : 26880 ki-lô-gam.

1: BC=BH+CH=4+9=13(cm)

Xét ΔHAB vuông tại H và ΔACB vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔHAB~ΔACB

=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)

=>\(BA^2=BH\cdot BC=4\cdot13=52\)

=>\(BA=\sqrt{52}=2\sqrt{13}\left(cm\right)\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC^2=13^2-\left(2\sqrt{13}\right)^2=117\)

=>\(AC=\sqrt{117}=3\sqrt{13}\left(cm\right)\)

2: ΔHAB~ΔACB

=>\(\dfrac{HA}{AC}=\dfrac{AB}{CB}\)

=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{2\sqrt{13}\cdot3\sqrt{13}}{13}=6\left(cm\right)\)

Xét tứ giác AKHE có \(\widehat{AKH}=\widehat{AEH}=\widehat{KAE}=90^0\)

nên AKHE là hình chữ nhật

=>AH=KE

=>KE=6(cm)

3: Xét ΔAKH vuông tại K và ΔAHB vuông tại H có

\(\widehat{HAB}\) chung

Do đó: ΔAKH~ΔAHB

=>\(\dfrac{AK}{AH}=\dfrac{AH}{AB}\)

=>\(AH^2=AK\cdot AB\left(1\right)\)

Xét ΔAEH vuông tại E và ΔAHC vuông tại H có

\(\widehat{EAH}\) chung

Do đó: ΔAEH~ΔAHC

=>\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)

=>\(AH^2=AE\cdot AC\left(2\right)\)

Từ (1),(2) suy ra \(AK\cdot AB=AE\cdot AC\)

=>\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)

Xét ΔAKE vuông tại A và ΔACB vuông tại A có

\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)

Do đó: ΔAKE~ΔACB

4: ta có: ΔABC vuông tại A

mà AI là đường trung tuyến

nên IA=IC

=>ΔIAC cân tại I

=>\(\widehat{IAC}=\widehat{ICA}\)

ΔAKE~ΔACB

=>\(\widehat{AEK}=\widehat{ABC}\)

Ta có: \(\widehat{AEK}+\widehat{IAC}=\widehat{ABC}+\widehat{ACB}=90^0\)

=>EK\(\perp\)AI tại N

1. Tính AB, AC:

• Áp dụng định lý Pitago trong tam giác vuông AHB:
  • AB² = AH² + HB²
  • AH² = AB² - HB²
• Áp dụng định lý Pitago trong tam giác vuông AHC:
  • AC² = AH² + HC²
  • AH² = AC² - HC²
• Từ hai phương trình trên, ta có: AB² - HB² = AC² - HC²
• Suy ra: AB² = AC² - HC² + HB²
• Thay số: AB² = AC² - 9² + 4² = AC² - 65
• Áp dụng định lý Pitago trong tam giác vuông ABC:
  • BC² = AB² + AC²
  • BC² = (AC² - 65) + AC² = 2AC² - 65
• Thay BC = HB + HC = 4 + 9 = 13
  • 13² = 2AC² - 65
  • 2AC² = 13² + 65 = 224
  • AC² = 112
  • AC = √112 = 4√7 cm
• Thay AC vào phương trình AB² = AC² - 65:
  • AB² = (4√7)² - 65 = 112 - 65 = 47
  • AB = √47 cm

2. Tính KE:

• Áp dụng định lý Pitago trong tam giác vuông AKE:
  • KE² = AK² + AE²
• Áp dụng định lý Pitago trong tam giác vuông AHB:
  • AK² = AH² - HK²
• Áp dụng định lý Pitago trong tam giác vuông AHC:
  • AE² = AH² - HE²
• Thay vào phương trình KE²:
  • KE² = (AH² - HK²) + (AH² - HE²) = 2AH² - (HK² + HE²)
• Ta có: HK + HE = BC = 13 cm
• Áp dụng định lý Pitago trong tam giác vuông HKE:
  • KE² = HK² + HE² = (HK + HE)² - 2HK.HE = 13² - 2HK.HE
• Suy ra: 2AH² - (HK² + HE²) = 13² - 2HK.HE
• 2AH² = 13² + 2HK.HE
• AH² = (13² + 2HK.HE) / 2
• Thay AH² = AB² - HB²:
  • AB² - HB² = (13² + 2HK.HE) / 2
  • 2(AB² - HB²) = 13² + 2HK.HE
  • 2HK.HE = 2(AB² - HB²) - 13²
  • HK.HE = (AB² - HB²) - 13²/2
  • HK.HE = (47 - 4²) - 13²/2 = -65/2
• Vì HK và HE đều dương nên HK.HE = -65/2 là vô lý.
• Vậy, không thể tính KE bằng cách này.

3. Chứng minh AB.AK = AE.AC; AKE ~ ACB:

• Chứng minh AB.AK = AE.AC:
  • Xét tam giác vuông AHB và tam giác vuông AHC, ta có:
    • Góc BAH = Góc CAH (cùng bằng 90 độ)
    • Góc ABH = Góc ACH (cùng phụ với góc BAH)
  • Suy ra tam giác AHB đồng dạng với tam giác AHC (g-g)
  • Do đó: AB/AC = AH/AH = 1
  • Suy ra: AB = AC
  • Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
    • Góc KAE = Góc CAB (cùng bằng 90 độ)
    • Góc AKE = Góc ACB (cùng phụ với góc KAE)
  • Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)
  • Do đó: AK/AC = AE/AB
  • Suy ra: AB.AK = AE.AC
• Chứng minh AKE ~ ACB:
  • Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
    • Góc KAE = Góc CAB (cùng bằng 90 độ)
    • Góc AKE = Góc ACB (cùng phụ với góc KAE)
  • Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)

4. Chứng minh AI vuông góc KE tại N:

• Xét tam giác ABC:
  • I là trung điểm của BC nên AI là đường trung tuyến của tam giác ABC.
• Xét tam giác AKE:
  • N là giao điểm của AI và KE nên N là trọng tâm của tam giác AKE.
• Theo tính chất trọng tâm của tam giác:
  • Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
  • Do đó: AN = 2/3 AI
• Xét tam giác vuông AHI:
  • AI là đường trung tuyến của tam giác vuông AHI nên AI = 1/2 HI.
• Suy ra:
  • AN = 2/3 AI = 2/3 * (1/2 HI) = 1/3 HI
  • Do đó: IN = AI - AN = 1/2 HI - 1/3 HI = 1/6 HI
• Xét tam giác vuông HKE:
  • N là trung điểm của KE nên HN là đường trung tuyến của tam giác vuông HKE.
• Theo tính chất đường trung tuyến của tam giác vuông:
  • Đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
  • Do đó: HN = 1/2 KE
• Suy ra:
  • IN = 1/6 HI = 1/2 HN
  • Do đó: HN = 3IN
• Xét tam giác HIN:
  • HN = 3IN nên tam giác HIN vuông tại I (định lý đảo của định lý Pytago).
• Kết luận:
  • AI vuông góc KE tại N.

Lưu ý:

• Trong bài toán này, không thể tính KE bằng cách sử dụng định lý Pitago trong tam giác vuông HKE vì HK.HE là một số âm.
• Việc chứng minh AB.AK = AE.AC và AKE ~ ACB là cần thiết để chứng minh AI vuông góc KE tại N.
• Việc chứng minh AI vuông góc KE tại N là một ứng dụng của tính chất trọng tâm của tam giác và tính chất đường trung tuyến của tam giác vuông.
•  

a) So với học sinh của cả lớp, 2 tổ chiếm:

\(\frac24\times100\%=50\%\)

b) Số học sinh của 2 tổ là:

\(36\times50\%=18\) (học sinh)

9hs

\(-1,25=-\dfrac{125}{100}=-\dfrac{5}{4}\)

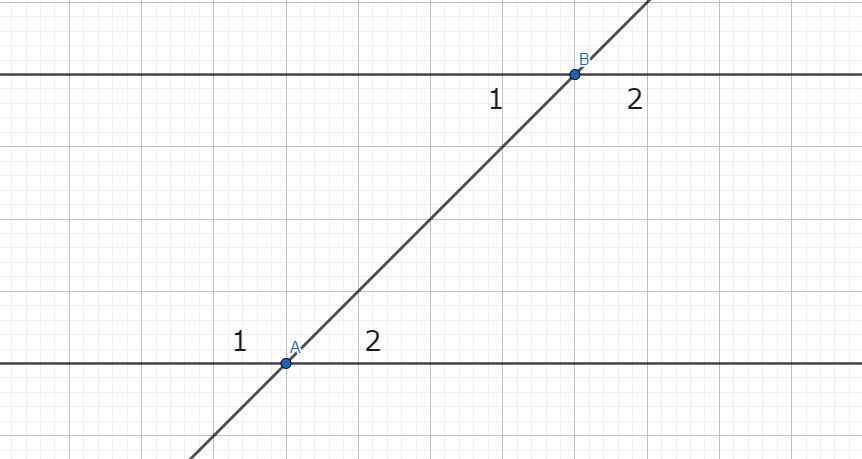 Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)

Mặt khác:

\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\) (hai cặp góc kề bù)

Mà \(\widehat{A_1}=\widehat{B_2}\) nên:

\(\widehat{A_2}=\widehat{B_1}\) Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì các cặp góc so le trong còn lại cũng bằng nhau.

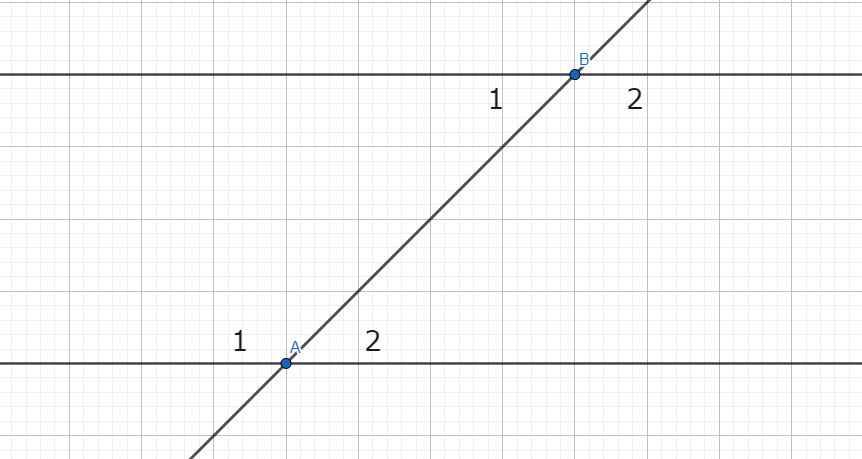Giả sử \(\widehat{A_1}\) và \(\widehat{B_2}\) là cặp góc so le trong đề bài cho.

Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)

Mặt khác:

\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)(hai cặp góc kề bù)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\)

Mà \(\widehat{A_1}=\widehat{B_2}\) nên:

\(\widehat{A_2}=\widehat{B_1}\) hay cặp góc so le trong còn lại bằng nhau

Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì cặp góc so le trong còn lại cũng bằng nhau.