Lời giải:

Gọi $I$ là trung điểm $BC$

$\Rightarrow BI=IC=\frac{BC}{2}$

Tam giác $BEC$ vuông tại $E$ nên trung tuyến $EI=\frac{BC}{2}$
Tam giác $BDC$ vuông tại $D$ nên trung tuyến $DI=\frac{BC}{2}$

$\Rightarrow BI=IC=EI=DI=\frac{BC}{2}$ nên $I$ là tâm đường tròn đi qua $B,C,D,E$. Bán kính đường tròn đi qua $B,C,E,D$ là $\frac{BC}{2}$

Đáp án D.

Hình vẽ:

Hệ thức nào em nhỉ?

Nếu \(\Delta>0\) thì có 2 nghiệm phân biệt
Nếu\(\Delta< 0\) thì vô nghiệm
Nếu\(\Delta=0\) Thì \(x_1=x_2\)
Này đơn giản dễ nhớ mà=))

 Δ≥0 thì phương trình có 2 nghiệm

a) Ta có \(M\left(1,m\right)\) và \(N\left(-3,n\right)\).

Vì \(M,N\in\left(P\right):y=\dfrac{1}{2}x^2\) nên ta suy ra \(m=\dfrac{1}{2};n=\dfrac{9}{2}\)

Gọi đường thẳng cần tìm là \(d:y=ax+b\). Vì \(d\) đi qua M và N nên ta có hệ pt sau:

 \(\left\{{}\begin{matrix}\dfrac{1}{2}=a+b\\\dfrac{9}{2}=-3a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=\dfrac{3}{2}\end{matrix}\right.\).

Vậy ptđt cần tìm là \(d:y=-x+\dfrac{3}{2}\)

b) Mình chưa hiểu đề bài lắm. Thế nào là "cắt parabol tại 2 điểm đạt GTNN"?

có hình ko cho xin với

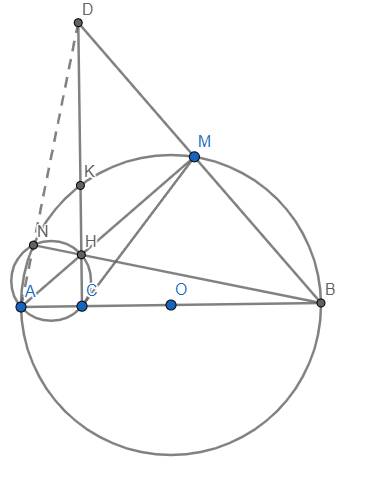
a) Xét đường tròn (O) có đường kính AB \(\Rightarrow\widehat{AMB}=90^o\)

\(\Rightarrow\widehat{AMD}=90^o\)

Lại có \(\widehat{ACD}=90^o\) nên tứ giác ACMD nội tiếp đường tròn (AD).

b) Tứ giác ACMD nội tiếp \(\Rightarrow\widehat{CAM}=\widehat{CDM}\) hay \(\widehat{CAH}=\widehat{DCB}\)

Từ đó dễ dàng chứng minh \(\Delta CAH~\Delta CDB\left(g.g\right)\)

\(\Rightarrow\dfrac{CA}{CD}=\dfrac{CH}{CB}\) \(\Rightarrow CA.CB=CH.CD\)

c) Ta thấy \(\widehat{ANH}=\widehat{ACH}=90^o\) nên tứ giác ANHC nội tiếp.

 Đồng thời \(\widehat{HMB}=\widehat{HCB}=90^o\) nên tứ giác HCBM nội tiếp.

 \(\Rightarrow\widehat{HCM}=\widehat{HBM}\).

 Từ đó dễ dàng suy ra \(\Delta DMC~\Delta DHB\left(g.g\right)\)

 \(\Rightarrow\dfrac{DM}{DH}=\dfrac{DC}{DB}\)

\(\Rightarrow DM.DB=DH.DC\)

\(\Rightarrow P_{D/\left(ANHC\right)}=P_{D/\left(O\right)}\)

\(\Rightarrow\) D thuộc trục đẳng phương của (ANHC) và (O)

\(\Rightarrow A,N,D\) thẳng hàng.

Gọi chiều dài lúc đầu là \(x\) (m); \(x>0\)

Thì chiều rộng lúc đầu là: 160: 2 - \(x\) = 80 - \(x\) 

Chiều rộng lúc sau là: (100% + 20%).(80- \(x\)) = 1,2.(80 - \(x\)) 

Chiều dài lúc sau là: (100%- 10%).\(x\)           = 0,9\(x\)

Theo bài ra ta có phương trình:

         \(\dfrac{1,2.\left(80-x\right)}{0,9x}\) = \(\dfrac{4}{5}\)  

         5.1,2.(80 - \(x\))  = 4.0,9\(x\)

                480 - 6\(x\) = 3,6\(x\)

                6\(x\) + 3,6\(x\) = 480

                   9,6\(x\)      = 480

                        \(x\)      = 480 : 9,6

                        \(x\)      = 50

Chiều rộng là 80 - 50 = 30 (m)

Diện tích hình chữ nhật lúc đầu là: 50 x 30 = 1500 (m²)

Kết luận: Diện tích hình chữ nhật lúc đầu là: 1500 m²