(11/4)^12:(-11/4)^11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(\dfrac{3}{7}\right)^2.\left(-7\right)^4\\ =\left(\dfrac{3}{7}\right)^2.7^4\\ =\left(\dfrac{3}{7}\right)^2.7^2.7^2\\ =9.49\\ =441\)

Bài 4
4a, 12,48 x 3,47 - 3,47 x 2,48
= 3,47 x ( 12,48 - 2,48)
= 3,47 x 10
= 34,7
4b, 128 x 68 + 16 x 256
= 128 x 68 + 16 x 2 x 128
= 128 x (68 + 32)
= 128 x 100
12800
4c, (7,29 + 9,34 + 8,27) - (7,34 + 6,27 + 5,29)
= 7,29 + 9,34 + 8,27 - 7,34 - 6,27 - 5,29
= (7,29 - 5,29) + (9,34 - 7,34) + (8,27 - 6,27)
= 2 + 2 + 2
= 6

2a,
(100 + 67) x 67 + (200 - 33) x 33
= 167 x 67 + 167 x 33
= 167 x (67 + 33)
= 167 x 100
= 16700
2b, 45,651 x 73 + 45,651 x 20 + 45,651 x 7
= 45,651 x (73 + 20 + 7)
= 45,651 x 100
= 4565,1

1a, 6,28 x 18,24 + 18,24 x 3,72
= 18,24 x (6,28 + 3,72)
= 18,24 x 10
= 182,4
b, 35,7 x 99 + 35 + 0,7
= 35,7 x 99 + 35,7
= 35,7 x (99 + 1)
= 35,7 x 100
= 3570

A = 101.102.103.104...108
A = 101+2+3+..+8
A = 1036

A = 1.2 + 2.3 + 3.4 + 4.5 + ... + 99.100 + 100.101
3.A = 1.2.3 + 2.3.3 +3.4.3 + ... + 100.101.3
3A= 1.2.3 + 2.3.(4 - 1) + 3.4.(5 - 2) + ... + 100.101.(102 - 99)
3A = 1.2.3 + 2.3.4 - 1.2.3 + 2.3.4 -3.4.5 + ... +99.100.101 -100.101.102
3A = 99.100.101
A = 99.100.101 : 3
A = 33.100.101
Vậy A = 33. 100 .101 = 333300
{[(100+101)+100]+[(103.104.105 ):106 ].[(107 :108).109].1010}.1011=???
{[(1+10)+100]+[(1K.10K.100K):1M].[(10M:100M).1B].10B}.100B
K= nghìn
M= triệu
B= tỷ


Hôm nay olm.vn sẽ hướng dẫn các em giải toán nâng cao lớp 7 bằng phương pháp hệ số bất định em nhé.
Vì ( \(x^3\) - \(x^2\) + a\(x\) + b): (\(x^2\) - 2\(x\) + 3) dư 6
Ta thấy đa thức bị chia bậc ba, đa thức chia bậc hai nên thương có dạng: c\(x\) + d vì hệ số cao nhất của đa thức bị chia là 1 nên c = 1
Theo bài ra ta có:
\(x^3\) - \(x^2\) + a\(x\) + b = (\(x^2\) - 2\(x\) + 3)(\(x\) + d) + 6
\(x^3\) - \(x^2\) + a\(x\) + b = \(x^3\) + d\(x^2\) - 2\(x^2\) - 2d\(x\) + 3\(x\) + 3d + 6
\(x^3\) - \(x^2\) + a\(x\) + b = \(x^{3^{ }}\) + (d - 2)\(x^2\) + (3 - 2d)\(x\) + 3d + 6
⇒ \(\left\{{}\begin{matrix}d-2=-1\\a=3-2d\\b=3d+6\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}d=1\\a=3-2\\b=3+6\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}d=1\\a=1\\b=9\end{matrix}\right.\)
Vậy a = 1; b = 9

a, \(\dfrac{\dfrac{-6}{7}+\dfrac{6}{19}-\dfrac{6}{31}}{\dfrac{9}{7}-\dfrac{9}{19}+\dfrac{9}{31}}\)
= \(\dfrac{-6.\left(\dfrac{1}{7}-\dfrac{1}{19}+\dfrac{1}{31}\right)}{9.\left(\dfrac{1}{7}-\dfrac{1}{19}+\dfrac{1}{31}\right)}\)
= - \(\dfrac{2}{3}\)
b, \(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{\dfrac{4}{9}-\dfrac{4}{7}-\dfrac{4}{11}}\)+ \(\dfrac{\dfrac{3}{5}-\dfrac{3}{25}-\dfrac{3}{125}-\dfrac{3}{625}}{\dfrac{4}{5}-\dfrac{4}{25}-\dfrac{4}{125}-\dfrac{4}{625}}\)
= \(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{4.(\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11})}\) + \(\dfrac{3.(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625})}{4.\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}\)
= \(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)
= 1


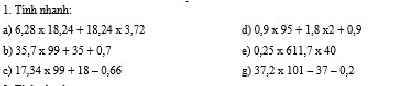
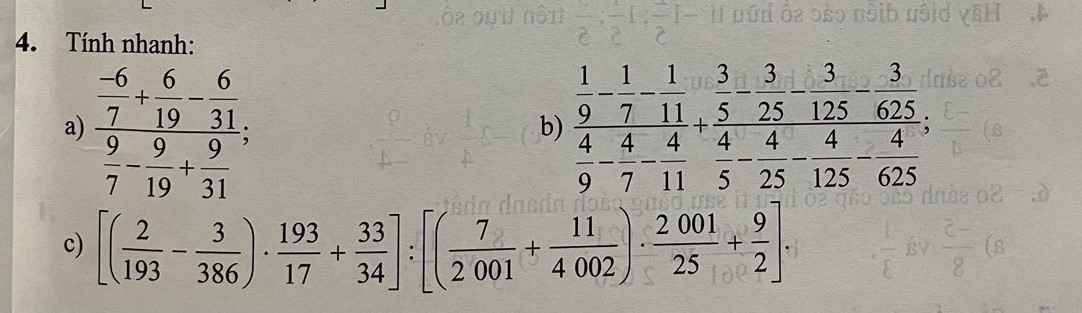
\(\left(\dfrac{11}{4}\right)^{12}:\left(-\dfrac{11}{4}\right)^{11}\)
\(=\left(-\dfrac{11}{4}\right)^{12}:\left(-\dfrac{11}{4}\right)^{11}\)
\(=\left(-\dfrac{11}{4}\right)^{12-11}\)
\(=\left(-\dfrac{11}{4}\right)^1\)
\(=-\dfrac{11}{4}\)
(11/4)^12:(-11/4)^11