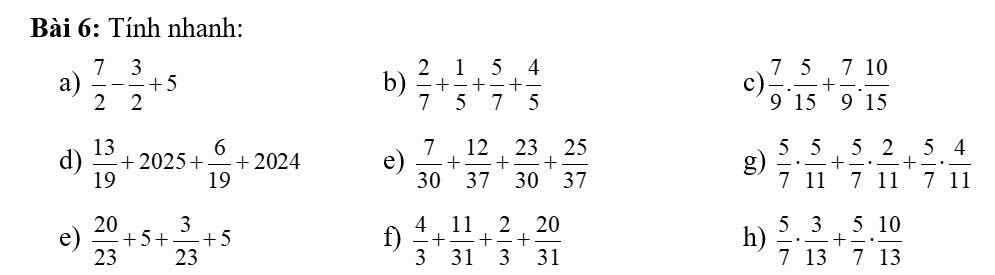
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi tổng số học sinh giỏi lớp 6;7;8 là x
Do x chia 3 dư 2, chia 4 dư 3, chia 53 dư 52
\(\Rightarrow x+1\) chia hết cho 3,4,53
\(\Rightarrow x+1\in BC\left(3;4;53\right)\)
Mà x nhỏ nhất
\(\Rightarrow x+1=BCNN\left(3;4;53\right)\)
\(\Rightarrow x+1=636\)
\(\Rightarrow x=635\)

\(3^x.3^{x+5}=3^{x+12}\)
\(3^{x+x+5}=3^{x+12}\)
\(3^{2x+5}=3^{x+12}\)
\(2x+5=x+12\)
\(2x-x=12-5\)
\(x=7\)

\(3^x.3^{x-2}=3^{100}\)
\(3^{x+x-2}=3^{100}\)
\(3^{2x-2}=3^{100}\)
\(2x-2=100\)
\(2x=102\)
\(x=51\)
\(3^x\cdot3^{x-2}=3^{100}\\ \Rightarrow3^{x+x-2}=3^{100}\\ \Rightarrow2x-2=100\\ \Rightarrow2x=102\\ \Rightarrow x=102:2\\ \Rightarrow x=51\)

Ngày thứ nhất, Minh đọc số trang sách là:
\(250\cdot\dfrac{2}{5}=100\) (trang)
Sau ngày thứ nhất, Minh còn lại số trang sách là:
\(250-100=150\) (trang)
Ngày thứ hai, Minh đọc số trang sách là:
\(150\cdot\dfrac{1}{3}=50\) (trang)
Minh phải đọc số trang thì hết quyển là:
\(250-100-50=100\) (trang)
Vậy: Minh phải độc số trang thì hết quyển là: \(100\) trang
Giải:
Số trang sách còn lại sau ngày thứ nhất là:
250 x (1 - \(\dfrac{2}{5}\)) = 150 (trang)
Số trang sách Minh còn phải đọc sau ngày thứ hai để hết quyển sách là:
150 x (1 - \(\dfrac{1}{3}\)) = 100 (trang)
Kết luận:...

a: \(\dfrac{4x^4+3x^3}{-x^3}+\dfrac{15x^2+6x}{3x}=0\)
=>\(-4x-3+5x+2=0\)
=>x-1=0
=>x=1
b: \(\left(3x^2-\dfrac{1}{3}x\right):x+\left(2-3x\right)^2:\left(3x-2\right)=0\)
=>\(3x-\dfrac{1}{3}+\dfrac{\left(3x-2\right)^2}{3x-2}=0\)
=>\(3x-\dfrac{1}{3}+3x-2=0\)
=>\(6x=\dfrac{7}{3}\)
=>\(x=\dfrac{7}{3}:6=\dfrac{7}{18}\)
c: \(6x^2-\left(2x+1\right)\left(3x-2\right)-x=-2\)
=>\(6x^2-\left(6x^2-4x+3x-2\right)-x+2=0\)
=>\(6x^2-6x^2+x+2-x+2=0\)
=>4=0(vô lý)
vậy: Phương trình vô nghiệm

\(x^2-2x+m=0\Leftrightarrow x^2-2x-3=-m-3\)
Từ đồ thị ta thấy:
a.
Phương trình vô nghiệm khi \(-m-3< -4\Rightarrow m>1\)
b.
Phương trình có nghiệm kép khi \(-m-3=-4\Rightarrow m=1\)
c.
Phương trình có 2 nghiệm pb khi:
\(-m-3>-4\Rightarrow m< 1\)
d.
Phương trình có 2 nghiệm pb thuộc \(\left[-1;3\right]\) khi: \(-4< m\le0\)
e.
Có 2 nghiệm pb ko thuộc \(\left[-1;3\right]\) khi \(m>0\)

\(25-\left(4+2\times y\right)=5\\ 4+2\times y=25-5\\4+2\times y=20\\ 2\times y=20-4\\ 2\times y=16\\ y=16:2\\ y=8\)
a: \(\dfrac{7}{2}-\dfrac{3}{2}+5=5+2=7\)
b: \(\dfrac{2}{7}+\dfrac{1}{5}+\dfrac{5}{7}+\dfrac{4}{5}\)
\(=\left(\dfrac{2}{7}+\dfrac{5}{7}\right)+\left(\dfrac{1}{5}+\dfrac{4}{5}\right)\)
=1+1=2
c: \(\dfrac{7}{9}\cdot\dfrac{5}{15}+\dfrac{7}{9}\cdot\dfrac{10}{15}\)
\(=\dfrac{7}{9}\left(\dfrac{5}{15}+\dfrac{10}{15}\right)\)
\(=\dfrac{7}{9}\cdot\dfrac{15}{15}=\dfrac{7}{9}\)
d: \(\dfrac{13}{19}+2025+\dfrac{6}{19}+2024\)
\(=\left(\dfrac{13}{19}+\dfrac{6}{19}\right)+\left(2025+2024\right)\)
=4049+1=4050
e: \(\dfrac{7}{30}+\dfrac{12}{37}+\dfrac{23}{30}+\dfrac{25}{37}\)
\(=\left(\dfrac{7}{30}+\dfrac{23}{30}\right)+\left(\dfrac{12}{37}+\dfrac{25}{37}\right)\)
\(=1+1=2\)
g: \(\dfrac{5}{7}\cdot\dfrac{5}{11}+\dfrac{5}{7}\cdot\dfrac{2}{11}+\dfrac{5}{7}\cdot\dfrac{4}{11}\)
\(=\dfrac{5}{7}\left(\dfrac{5}{11}+\dfrac{2}{11}+\dfrac{4}{11}\right)\)
\(=\dfrac{5}{7}\cdot\dfrac{11}{11}=\dfrac{5}{7}\)
e: \(\dfrac{20}{23}+5+\dfrac{3}{23}+5\)
\(=\left(\dfrac{20}{23}+\dfrac{3}{23}\right)+5+5\)
=1+10=11
f: \(\dfrac{4}{3}+\dfrac{11}{31}+\dfrac{2}{3}+\dfrac{20}{31}\)
\(=\left(\dfrac{4}{3}+\dfrac{2}{3}\right)+\left(\dfrac{11}{31}+\dfrac{20}{31}\right)\)
=2+1=3
h: \(\dfrac{5}{7}\cdot\dfrac{3}{13}+\dfrac{5}{7}\cdot\dfrac{10}{13}\)
\(=\dfrac{5}{7}\left(\dfrac{3}{13}+\dfrac{10}{13}\right)\)
\(=\dfrac{5}{7}\cdot\dfrac{13}{13}=\dfrac{5}{7}\)