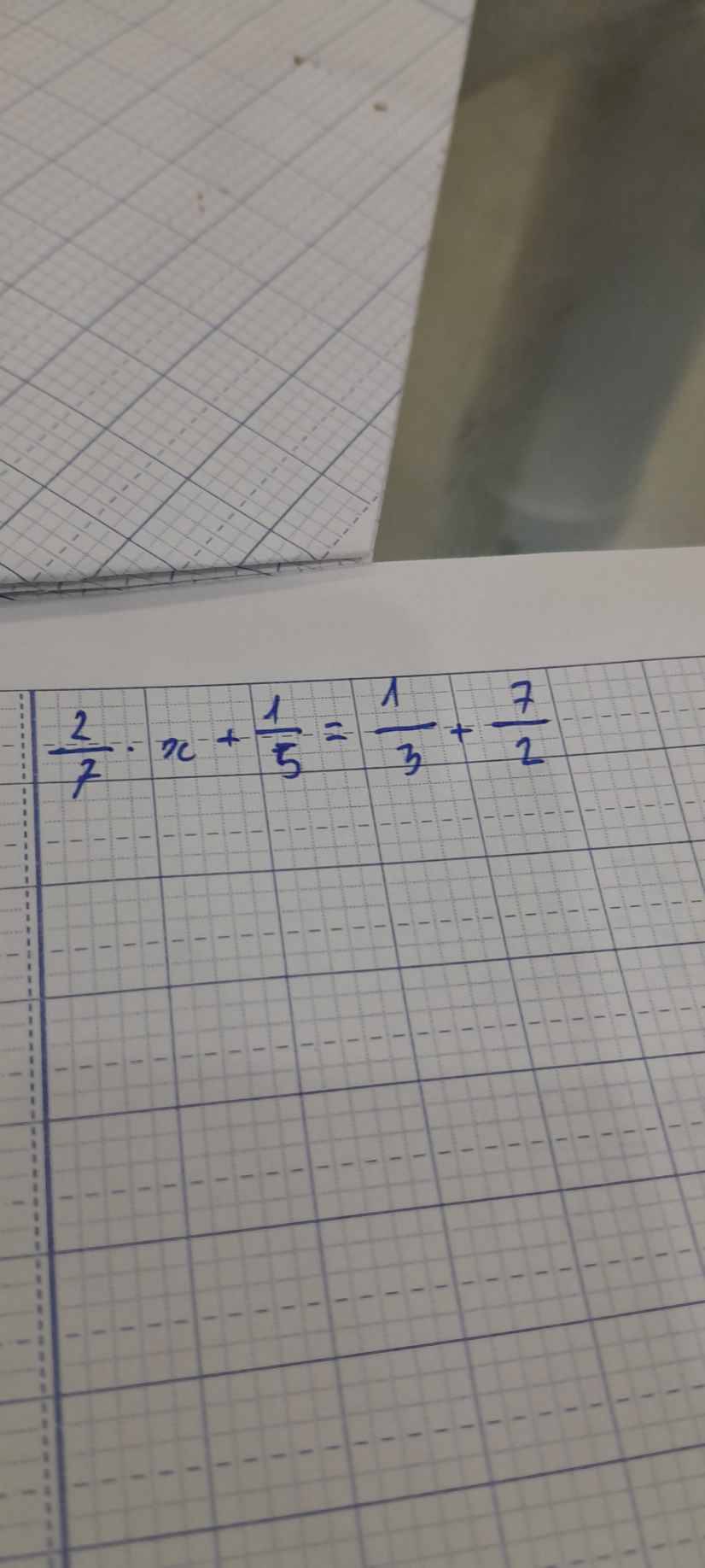tìm giá trị lớn nhất của P = \(\dfrac{|x-2022|-|x-2023|+|x-2024|+2022}{|x-2022|+|x-2023|+|x-2024|}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(k^2=\left(m+1\right)\left(m^2+2m\right)\) là số chính phương
\(\Rightarrow k^2=m\left(m+1\right)\left(m+2\right)\ge0\)
Lập bảng xét dấu
| \(m\) | \(-2\) \(-1\) \(0\) |
| \(m\) | \(-\) \(|\) \(-\) \(|\) \(-\) \(0\) \(+\) |
| \(m+1\) | \(-\) \(|\) \(-\) \(0\) \(+\) \(|\) \(+\) |
| \(m+2\) | \(-\) \(0\) \(+\) \(|\) \(+\) \(|\) \(+\) |
| \(m\left(m+1\right)\left(m+2\right)\) | \(-\) \(0\) \(+\) \(0\) \(-\) \(0\) \(+\) |
\(\Rightarrow\left[{}\begin{matrix}-2\le m\le0\\m>0\end{matrix}\right.\)
\(TH1:\) \(-2\le m\le0\Rightarrow m\in\left\{-2;-1;0\right\}\) thỏa mãn \(k^2=0\ge0\)
\(TH2:\) \(m>0\)
\(k^2=\left(m+1\right)\left(m^2+2m\right)\)
\(d=UC\left(m+1;m^2+2m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}m+1⋮d\\m^2+2m⋮d\end{matrix}\right.\)
\(\Rightarrow m^2+2m-2\left(m+1\right)⋮d\)
\(\Rightarrow m^2+2m-2m-1⋮d\)
\(\Rightarrow-1⋮d\)
\(\Rightarrow d\in\left\{-1;1\right\}\)
\(\Rightarrow\left(m+1\right)\left(m^2+2m\right)\) là số chính phương khi chúng là số chính phương.
Ta lại có :
\(\left(m+1\right)\left(m^2+2m\right)=m\left(m+1\right)\left(m+2\right)\) là tích của 3 số liên tiếp nhau không phải là số chính phương khi m>0
Vậy \(m\in\left\{-2;-1;0\right\}\) thỏa mãn đề bài

Lời giải:
$\frac{2}{7}x+\frac{1}{5}=\frac{1}{3}+\frac{7}{2}$
$\frac{2}{7}x+\frac{1}{5}=\frac{23}{6}$
$\frac{2}{7}x=\frac{23}{6}-\frac{1}{5}$
$\frac{2}{7}x=\frac{109}{30}$
$x=\frac{109}{30}: \frac{2}{7}=\frac{763}{60}$

Lời giải:
$\frac{1}{2}x+\frac{1}{5}=\frac{1}{3}+\frac{7}{2}$
$\frac{1}{2}x+\frac{1}{5}=\frac{23}{6}$
$\frac{1}{2}x=\frac{23}{6}-\frac{1}{5}=\frac{109}{30}$
$x=\frac{109}{30}: \frac{1}{2}=\frac{109}{15}$

\(\sqrt[]{x+2}=-100\)
vì \(\sqrt[]{x+2}\ge0\)
Nên phương trình trên vô nghiệm

a) Ta đặt \(P\left(x\right)=x^2+x+1\)
\(P\left(x\right)=x^2+x-20+21\)
\(P\left(x\right)=\left(x+5\right)\left(x-4\right)+21\)
Giả sử tồn tại số tự nhiên \(x\) mà \(P\left(x\right)⋮9\) \(\Rightarrow P\left(x\right)⋮3\). Do \(21⋮3\) nên \(\left(x+5\right)\left(x-4\right)⋮3\).
Mà 3 là số nguyên tố nên suy ra \(\left[{}\begin{matrix}x+5⋮3\\x-4⋮3\end{matrix}\right.\)
Nếu \(x+5⋮3\) thì suy ra \(x-4=\left(x+5\right)-9⋮3\) \(\Rightarrow\left(x+4\right)\left(x-5\right)⋮9\)
Lại có \(P\left(x\right)⋮9\) nên \(21⋮9\), vô lí.
Nếu \(x-4⋮3\) thì suy ra \(x+5=\left(x-4\right)+9⋮3\) \(\Rightarrow\left(x+4\right)\left(x-5\right)⋮9\)
Lại có \(P\left(x\right)⋮9\) nên \(21⋮9\), vô lí.
Vậy điều giả sử là sai \(\Rightarrow x^2+x+1⋮̸9\)
b) Vì \(x^2+x+1⋮̸9\) nên \(y\le1\Rightarrow y\in\left\{0;1\right\}\)
Nếu \(y=0\Rightarrow x^2+x+1=1\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Nếu \(y=1\) \(\Rightarrow x^2+x+1=3\)
\(\Leftrightarrow x^2+x-2=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)
Vậy ta tìm được các cặp số (x; y) thỏa ycbt là \(\left(0;0\right);\left(1;1\right)\)
a) Ta đặt
�
(
�
)
=
�
2
+
�
+
1
P(x)=x
2
+x+1
�
(
�
)
=
�
2
+
�
−
20
+
21
P(x)=x
2
+x−20+21
�
(
�
)
=
(
�
+
5
)
(
�
−
4
)
+
21
P(x)=(x+5)(x−4)+21
Giả sử tồn tại số tự nhiên
�
x mà
�
(
�
)
⋮
9
P(x)⋮9
⇒
�
(
�
)
⋮
3
⇒P(x)⋮3. Do
21
⋮
3
21⋮3 nên
(
�
+
5
)
(
�
−
4
)
⋮
3
(x+5)(x−4)⋮3.
Mà 3 là số nguyên tố nên suy ra
[
�
+
5
⋮
3
�
−
4
⋮
3
x+5⋮3
x−4⋮3
Nếu
�
+
5
⋮
3
x+5⋮3 thì suy ra
�
−
4
=
(
�
+
5
)
−
9
⋮
3
x−4=(x+5)−9⋮3
⇒
(
�
+
4
)
(
�
−
5
)
⋮
9
⇒(x+4)(x−5)⋮9
Lại có
�
(
�
)
⋮
9
P(x)⋮9 nên
21
⋮
9
21⋮9, vô lí.
Nếu
�
−
4
⋮
3
x−4⋮3 thì suy ra
�
+
5
=
(
�
−
4
)
+
9
⋮
3
x+5=(x−4)+9⋮3
⇒
(
�
+
4
)
(
�
−
5
)
⋮
9
⇒(x+4)(x−5)⋮9
Lại có
�
(
�
)
⋮
9
P(x)⋮9 nên
21
⋮
9
21⋮9, vô lí.
Vậy điều giả sử là sai \Rightarrow x^2+x+1⋮̸9
b) Vì x^2+x+1⋮̸9 nên
�
≤
1
⇒
�
∈
{
0
;
1
}
y≤1⇒y∈{0;1}
Nếu
�
=
0
⇒
�
2
+
�
+
1
=
1
y=0⇒x
2
+x+1=1
⇔
�
(
�
+
1
)
=
0
⇔x(x+1)=0
⇔
[
�
=
0
(
�
ℎ
ậ
�
)
�
=
−
1
(
�
�
ạ
�
)
⇔[
x=0(nhận)
x=−1(loại)
Nếu
�
=
1
y=1
⇒
�
2
+
�
+
1
=
3
⇒x
2
+x+1=3
⇔
�
2
+
�
−
2
=
0
⇔x
2
+x−2=0
⇔
(
�
−
1
)
(
�
+
2
)
=
0
⇔(x−1)(x+2)=0
⇔
[
�
=
1
(
�
ℎ
ậ
�
)
�
=
−
2
(
�
�
ạ
�
)
⇔[
x=1(nhận)
x=−2(loại)
Vậy ta tìm được các cặp số (x; y) thỏa ycbt là
(
0
;
0
)
;
(
1
;
1
)
(0;0);(1;1)

Để chứng minh rằng ba điểm B, A và C thẳng hàng, chúng ta cần sử dụng các thông tin đã cho và các quy tắc trong hình học.
Gọi G là giao điểm của đường thẳng FA và đường thẳng CE.
Vì tam giác EFM vuông tại E, nên ta có: ∠EMF = 90° Vì FA là phân giác của ∠EMF, nên ta có: ∠FAG = ∠GEM Vì CE là tia đối của tia EF,
nên ta có: ∠GEC = ∠FEM Vì CE = MB, nên ta có: ∠ECG = ∠MBC
Vì ∠GEC = ∠FEM và ∠ECG = ∠MBC, nên ta có: ∠FEM = ∠MBC Vì ∠FAG = ∠GEM và ∠FEM = ∠MBC,
nên ta có: ∠FAG = ∠MBC
Vậy ta có hai góc cùng nhìn trên cùng một đường thẳng, nên ta có: B, A, C thẳng hàng.
Vậy ta đã chứng minh được rằng ba điểm B, A và C thẳng hàng.