Giúp em nhanh với

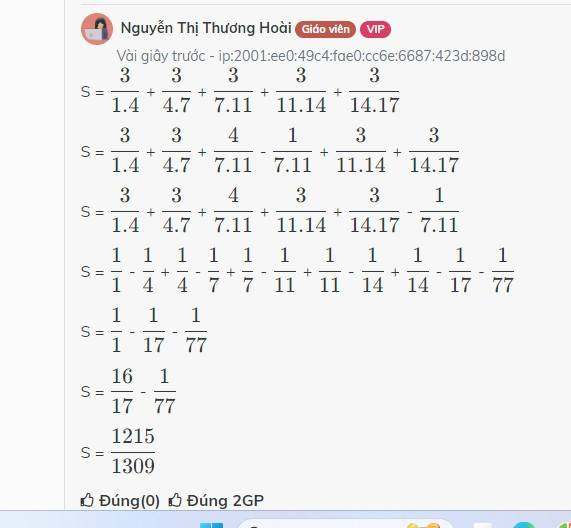
S = \(\dfrac{3}{1\times4}\) + \(\dfrac{3}{4\times7}\) + \(\dfrac{3}{7\times11}\) + \(\dfrac{3}{11\times14}\) + \(\dfrac{3}{14\times17}\)

S = \(\dfrac{3}{1.4}\) + \(\dfrac{3}{4.7}\) + \(\dfrac{4}{7.11}\) + \(\dfrac{3}{11.14}\) +\(\dfrac{3}{14.17}\) - \(\dfrac{1}{7.11}\)

S = \(\dfrac{1}{1}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{11}\) + \(\dfrac{1}{11}\) - \(\dfrac{1}{14}\) + \(\dfrac{1}{14}\) - \(\dfrac{1}{17}\) - \(\dfrac{1}{7.11}\)

S = \(\dfrac{1}{1}\) - \(\dfrac{1}{17}\) - \(\dfrac{1}{77}\)

S =  \(\dfrac{16}{17}\) - \(\dfrac{1}{77}\)

S = \(\dfrac{1215}{1309}\)

S = \(\dfrac{3}{1.4}\) + \(\dfrac{3}{4.7}\) + \(\dfrac{3}{7.11}\) + \(\dfrac{3}{11.14}\) + \(\dfrac{3}{14.17}\)

S = \(\dfrac{3}{1.4}\) + \(\dfrac{3}{4.7}\) + \(\dfrac{4}{7.11}\) + \(\dfrac{3}{11.14}\) + \(\dfrac{3}{14.17}\) - \(\dfrac{1}{7.11}\)

S = \(\dfrac{1}{1}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\)  - \(\dfrac{1}{7}\) + \(\dfrac{1}{11}\) - \(\dfrac{1}{14}\) + \(\dfrac{1}{14}\) - \(\dfrac{1}{17}\) - \(\dfrac{1}{77}\)

S = \(\dfrac{1}{1}\) - \(\dfrac{1}{17}\) - \(\dfrac{1}{77}\)

S = \(\dfrac{16}{17}\) - \(\dfrac{1}{77}\)

S = \(\dfrac{1215}{1309}\)

S = \(\dfrac{3}{1.4}\) + \(\dfrac{3}{4.7}\) + \(\dfrac{3}{7.11}\) + \(\dfrac{3}{11.14}\) + \(\dfrac{3}{14.17}\)

S = \(\dfrac{3}{1.4}\) + \(\dfrac{3}{4.7}\) + \(\dfrac{4}{7.11}\) + \(\dfrac{3}{11.14}\) + \(\dfrac{3}{14.17}\) - \(\dfrac{1}{7.11}\)

S = \(\dfrac{1}{1}\)-\(\dfrac{1}{4}\)+\(\dfrac{1}{4}\)-\(\dfrac{1}{7}\)+\(\dfrac{1}{7}\)-\(\dfrac{1}{11}\)+\(\dfrac{1}{11}\)-\(\dfrac{1}{14}\) + \(\dfrac{1}{14}\) - \(\dfrac{1}{17}\) - \(\dfrac{1}{77}\) 

S = 1 - \(\dfrac{1}{17}\) - \(\dfrac{1}{77}\)

S = \(\dfrac{16}{17}\) - \(\dfrac{1}{77}\)

S = \(\dfrac{1215}{1309}\)

Đề sai, như vậy không tính nhanh được nhé em!

Bạn xem đã viết đúng đề chưa nhỉ. Các thừa số đang cách nhau 3 đơn vị tự nhiên xuất hiện 7 x 11 có 2 thừa số cách nhau 4 đơn vị?

S = \(\dfrac{3}{1.4}\) + \(\dfrac{3}{4.7}\) + \(\dfrac{3}{7.11}\) + \(\dfrac{3}{11.14}\) + \(\dfrac{3}{14.17}\)

S = \(\dfrac{3}{1.4}\) + \(\dfrac{3}{4.7}\) + \(\dfrac{4}{7.11}\) - \(\dfrac{1}{7.11}\) + \(\dfrac{3}{11.14}\) + \(\dfrac{3}{14.17}\)

S = \(\dfrac{3}{1.4}\) + \(\dfrac{3}{4.7}\) + \(\dfrac{4}{7.11}\) + \(\dfrac{3}{11.14}\) + \(\dfrac{3}{14.17}\) - \(\dfrac{1}{7.11}\)

S = \(\dfrac{1}{1}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{11}\) + \(\dfrac{1}{11}\) - \(\dfrac{1}{14}\) + \(\dfrac{1}{14}\) - \(\dfrac{1}{17}\) - \(\dfrac{1}{77}\)

S = \(\dfrac{1}{1}\) - \(\dfrac{1}{17}\) - \(\dfrac{1}{77}\)

S = \(\dfrac{16}{17}\) - \(\dfrac{1}{77}\)

S = \(\dfrac{1215}{1309}\)

Bài 1:

a; \(\dfrac{5}{18}\) + \(\dfrac{8}{19}\) - \(\dfrac{7}{21}\) + (- \(\dfrac{10}{36}\) + \(\dfrac{11}{19}\)  + \(\dfrac{1}{3}\)) - \(\dfrac{5}{8}\)

=  \(\dfrac{5}{18}\) + \(\dfrac{8}{19}\) - \(\dfrac{1}{3}\) -\(\dfrac{10}{36}\) + \(\dfrac{11}{19}\) + \(\dfrac{1}{3}\) - \(\dfrac{5}{8}\)

= (\(\dfrac{5}{18}\) - \(\dfrac{10}{36}\)) + (\(\dfrac{8}{19}\) + \(\dfrac{11}{19}\)) - (\(\dfrac{1}{3}\) - \(\dfrac{1}{3}\)) - \(\dfrac{5}{8}\)

= (\(\dfrac{5}{18}\) - \(\dfrac{5}{18}\)) + \(\dfrac{19}{19}\) - 0 - \(\dfrac{5}{8}\)

= 0 + 1 - \(\dfrac{5}{8}\)

= \(\dfrac{3}{8}\)

b; \(\dfrac{1}{13}\) + (\(\dfrac{-5}{18}\) - \(\dfrac{1}{13}\) + \(\dfrac{12}{17}\)) - (\(\dfrac{12}{17}\) - \(\dfrac{5}{18}\) + \(\dfrac{7}{5}\))

= \(\dfrac{1}{13}\) - \(\dfrac{5}{18}\) - \(\dfrac{1}{13}\) + \(\dfrac{12}{17}\) - \(\dfrac{12}{17}\) + \(\dfrac{5}{18}\) - \(\dfrac{7}{5}\)

= (\(\dfrac{1}{13}\) - \(\dfrac{1}{13}\)) + (\(\dfrac{12}{17}\) - \(\dfrac{12}{17}\)) + (-\(\dfrac{5}{18}\) + \(\dfrac{5}{18}\)) - \(\dfrac{7}{5}\)

= 0 + 0 + 0 - \(\dfrac{7}{5}\)

= - \(\dfrac{7}{5}\)

Bài 1 c;

   \(\dfrac{15}{14}\) - (\(\dfrac{17}{23}\) - \(\dfrac{80}{87}\) + \(\dfrac{5}{4}\)) + (\(\dfrac{17}{23}\) - \(\dfrac{15}{14}\) + \(\dfrac{1}{4}\))

=  \(\dfrac{15}{14}\) - \(\dfrac{17}{23}\) + \(\dfrac{80}{87}\) - \(\dfrac{5}{4}\) + \(\dfrac{17}{23}\) - \(\dfrac{15}{14}\) + \(\dfrac{1}{4}\)

= (\(\dfrac{15}{14}-\dfrac{15}{14}\)) + (\(-\dfrac{17}{23}+\dfrac{17}{23}\)) - (\(\dfrac{5}{4}\) - \(\dfrac{1}{4}\)) + \(\dfrac{80}{87}\)

= 0 + 0 - 1 + \(\dfrac{80}{87}\)

= - \(\dfrac{7}{87}\)

gọi d=ƯCLN                ta có 3n chia hết cho d

                          3n+1 chia hết cho d

suy ra

(3n+1)-(3n)

hay

1 chia hết cho d

Phân số trên là phân số tối giản vì tử và mẫu là hai số liên tiếp.

CHÚC BẠN HỌC TỐT NHÉ!!!!

Lần sau bạn để đúng môn học nhé.

gọi tử của ps ban đầu là x ( x thuộc Z , x khác -14 )

=> mẫu của ps ban đầu là x+14

=> phân số ban đầu là : \(\dfrac{x}{x+14}\)

vì ps sau khi rút gọn là 993/1000 nên :

\(\dfrac{x}{x+14}=\dfrac{993}{1000}\)

=> 1000x = 993 ( x+14)

<=> 1000x = 993x + 13902

<=> 7x = 13902 

=> x = 1986 => tử số là 1986 => mẫu số của ps ban đầu là 1986+14=2000

=> ps ban đầu là 1986/2000