bạn để đúng lớp nhé.

Bài này ở lớp 5 nhé.

Mình nghĩ thế

2

2

Olm chào em, để xem lại câu hỏi cũ của em mà em đã từng hỏi trên olm thì em làm theo hướng dẫn sau:

               Từ trang hỏi đáp olm em kích vào câu hỏi của tôi như hình minh họa

Vậy là em đã tìm được câu hỏi cũ của em rồi đó.

Nhi đ nh

1 + 1 = 2

sao

Để giải bài toán này, ta sẽ giải phương trình: ABCD x 4 = DCBA Ta biểu diễn số ABCD dưới dạng 1000A + 100B + 10C + D và số DCBA dưới dạng 1000D + 100C + 10B + A. Vậy phương trình trở thành: 1000A + 100B + 10C + D = 1000D + 100C + 10B + A Chuyển các thành phần về cùng một phía ta được: 999A - 90B - 90C + 999D = 0 999(A - D) - 90(B - C) = 0 Vì A, B, C, D là các chữ số từ 0 đến 9 nên ta có thể thử từng trường hợp để tìm ra kết quả. Dễ dàng thấy rằng A = 2, B = 1, C = 7, D = 8 thỏa mãn phương trình trên. Vậy số ABCD = 2178.

Đáp án: D.3
Giải thích:

Để tìm cực trị của hàm hợp \( g(x) = f(x^2 - 2x - 1) \), ta cần thực hiện các bước sau:

1. Tìm điểm cực trị của hàm số \( f(x^2 - 2x - 1) \).
2. Phân tích số điểm cực trị của \( f(x^2 - 2x - 1) \) dựa trên đồ thị của \( f'(x) \).

Trước hết, để tìm điểm cực trị của hàm số \( f(x^2 - 2x - 1) \), ta cần tìm đạo hàm của \( g(x) \), sau đó giải phương trình \( g'(x) = 0 \) để tìm các điểm mà đạo hàm bằng 0.

Đạo hàm của \( g(x) = f(x^2 - 2x - 1) \):
\[ g'(x) = f'(x^2 - 2x - 1) \cdot (2x - 2) \]

Bây giờ, ta cần giải phương trình \( g'(x) = 0 \) để tìm điểm mà \( g(x) \) có đạo hàm bằng 0:
\[ f'(x^2 - 2x - 1) \cdot (2x - 2) = 0 \]

Điều này có nghĩa là hoặc \( f'(x^2 - 2x - 1) = 0 \) hoặc \( 2x - 2 = 0 \).

\( 2x - 2 = 0 \) khi \( x = 1 \).

Sau khi tìm \( x \), ta cần kiểm tra xem các giá trị của \( x \) khi đặt vào \( f'(x^2 - 2x - 1) \) tạo ra bao nhiêu điểm cực trị trên đồ thị của \( f'(x) \). Số lượng điểm cực trị của hàm số \( f(x) \) khi nhân với hệ số 2x-2 là số lượng điểm cực trị của hàm số \( f(x) \) bị tịnh tiến sang phải 1 đơn vị. Điều này có nghĩa là số điểm cực trị của \( g(x) \) sẽ giống với số điểm cực trị của \( f(x) \).

Vậy, đáp án là \(\mathbf{D. 3}\).

P/s: Lỗi font hơi nhiều

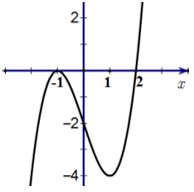
Từ đồ thị \(\Rightarrow\) hàm \(f\left(x\right)\) có 1 cực trị tại \(x=2\)

\(g'\left(x\right)=\left(2x-2\right).f'\left(x^2-2x-1\right)\)

\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}2x-2=0\\f'\left(x^2-2x-1\right)=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\x^2-2x-1=2\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=3\end{matrix}\right.\)

Vậy hàm \(g\left(x\right)\) có 3 cực trị