Thay a=1/3;b=3/5 vào A, ta được:

\(A=3\cdot\dfrac{1}{3}-\dfrac{1}{3}\cdot\dfrac{3}{5}+\dfrac{1}{2}\cdot\dfrac{1}{3}\cdot\dfrac{3}{5}\)

\(=1-\dfrac{1}{5}+\dfrac{1}{10}=\dfrac{4}{5}+\dfrac{1}{10}=\dfrac{9}{10}\)

\(C=\dfrac{5}{2\cdot7}+\dfrac{16}{7\cdot9}-\dfrac{2}{9\cdot11}-\dfrac{29}{1\cdot11}\)

\(=\dfrac{1}{2}-\dfrac{1}{7}+\dfrac{1}{7}+\dfrac{1}{9}-\dfrac{1}{9}+\dfrac{1}{11}-\dfrac{29}{11}\)

\(=\dfrac{1}{2}-\dfrac{28}{11}=\dfrac{11-56}{22}=\dfrac{-45}{22}< \dfrac{1}{3}\)

67

Ta có:

\(\left|x-5\right|+\left|2-4x\right|=\left|x-5\right|+\left|\dfrac{1}{2}-x\right|+3\left|\dfrac{1}{2}-x\right|\)

Mà \(\left|x-5\right|+\left|\dfrac{1}{2}-x\right|\ge\left|x-5+\dfrac{1}{2}-x\right|=\dfrac{9}{2}>4\)

\(\Rightarrow\left|x-5\right|+\left|2-4x\right|\ge4+3\left|\dfrac{1}{2}-x\right|>4>3\)

Vậy pt đã cho vô nghiệm

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

b: ΔAMB=ΔAMC

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

=>AD\(\perp\)BC tại M

Xét ΔMAB vuông tại M và ΔMDC vuông tại M có

MA=MD

MB=MC

Do đó: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)

=>AB//DC

c: ta có: ME\(\perp\)AB

AB//CD

Do đó: ME\(\perp\)CD

mà MF\(\perp\)CD

và ME,MF có điểm chung là M
nên M,E,F thẳng hàng

Xét ΔMEB vuông tại E và ΔMFC vuông tại F có

MB=MC

\(\widehat{MBE}=\widehat{MCF}\)(cmt)

Do đó: ΔMEB=ΔMFC

=>ME=MF

=>M là trung điểm của EF

TH1: \(-\dfrac{1}{2}\le x\le\dfrac{5}{3}\)

\(\left(2x+1\right)+\left(5-3x\right)=6\\ =>2x+1+5-3x=6\\ =>\left(2x-3x\right)+6=6\\ =>x=0\left(tm\right)\)

TH2: \(x>\dfrac{5}{3}\)

\(\left(2x+1\right)-\left(5-3x\right)=6\\ =>2x+1-5+3x=6\\ =>2x+3x=6-1+5\\ =>5x=10\\ =>x=\dfrac{10}{5}=2\left(tm\right)\)

TH3: \(x< -\dfrac{1}{2}\)

\(-\left(2x+1\right)+\left(5-3x\right)=6\\ =>-2x-1+5-3x=6\\ =>-2x-3x+4=6\\ =>-5x=6-4=2\\ =>x=-\dfrac{2}{5}\left(ktm\right)\)

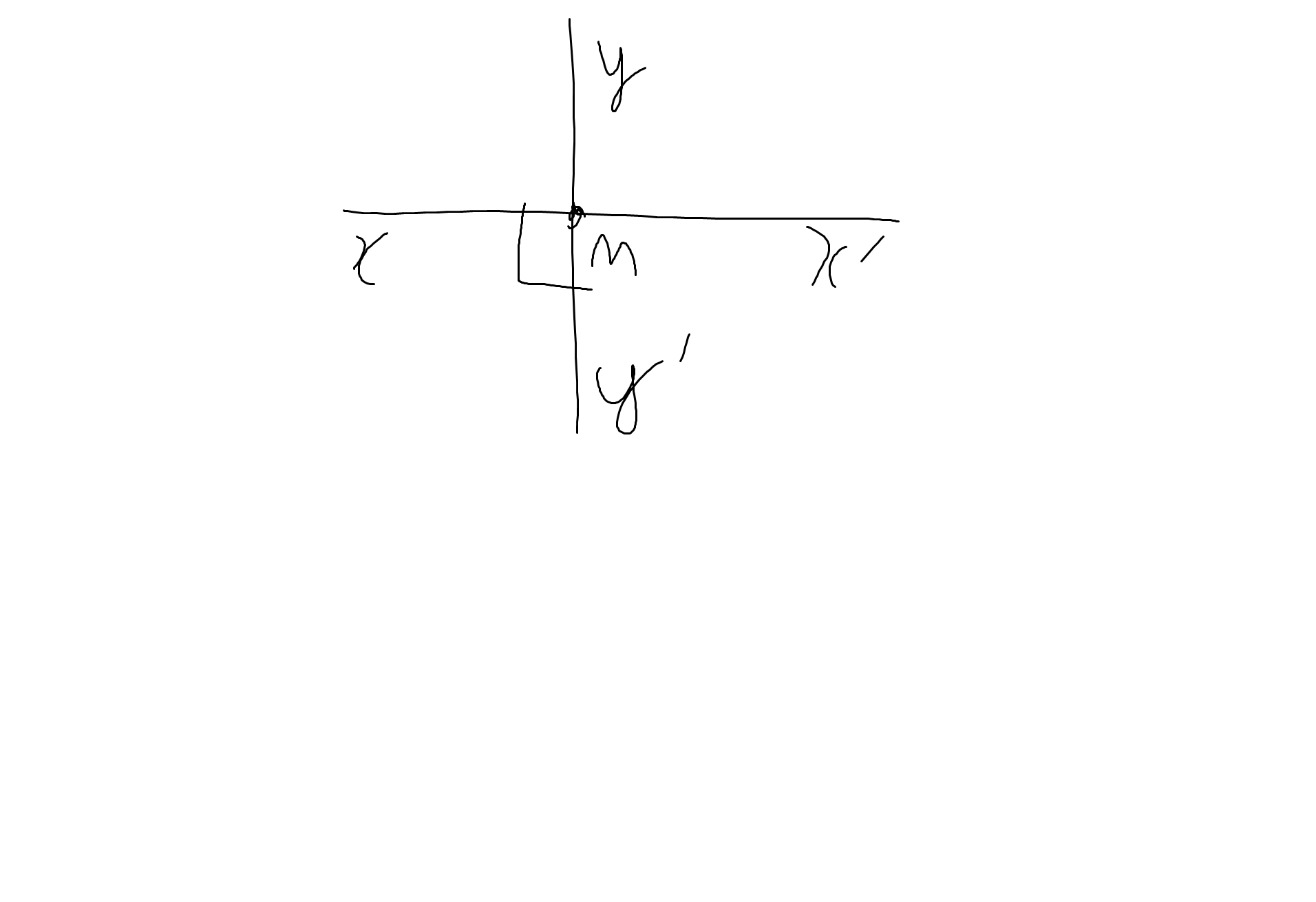
Ta có: \(\widehat{xMy'}=\widehat{x'My}\)(hai góc đối đỉnh)

mà \(\widehat{xMy'}=90^0\)

nên \(\widehat{x'My}=90^0\)

Ta có: \(\widehat{xMy'}+\widehat{x'My'}=180^0\)(hai góc kề bù)

=>\(\widehat{x'My'}=180^0-90^0=90^0\)

Ta có: \(\widehat{xMy}=\widehat{x'My'}\)(hai góc đối đỉnh)

mà \(\widehat{x'My'}=90^0\)

nên \(\widehat{xMy}=90^0\)

Bạn kiểm tra lại đề nhé.

\(\left(-\dfrac{3}{5}\right)^2.\dfrac{5}{11}+\dfrac{9}{25}.\left(-\dfrac{16}{11}\right)\)

\(=\dfrac{9}{25}.\dfrac{5}{11}+\dfrac{9}{25}.\left(-\dfrac{16}{11}\right)\)

\(=\dfrac{9}{25}.\left[\dfrac{5}{11}+\left(-\dfrac{16}{11}\right)\right]\)

\(=\dfrac{9}{25}.\left(-1\right)\)

\(=-\dfrac{9}{25}\)

7\(x\).2 hay 7\(x^2\) vậy em?

7x^2 ạ