 bài này làm ntn ạ
bài này làm ntn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔCHB vuông tại H và ΔCBA vuông tại B có
\(\widehat{HCB}\) chung
Do đó: ΔCHB~ΔCBA
b:
Xét ΔAHB vuông tại H và ΔABC vuông tại B có
\(\widehat{HAB}\) chung
Do đó: ΔAHB~ΔABC
=>\(\dfrac{AH}{AB}=\dfrac{AB}{AC}\)
=>\(AB^2=AH\cdot AC\)
c: ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(AC=\sqrt{15^2+20^2}=25\left(cm\right)\)
ΔAHB~ΔABC
=>\(\dfrac{BH}{BC}=\dfrac{BA}{AC}\)
=>\(BH=\dfrac{AB\cdot BC}{AC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
d: Xét ΔBKH vuông tại K và ΔBHA vuông tại H có
\(\widehat{KBH}\) chung
Do đó: ΔBKH~ΔBHA
=>\(\dfrac{BK}{BH}=\dfrac{BH}{BA}\)
=>\(BH^2=BK\cdot BA\left(1\right)\)
Xét ΔBIH vuông tại I và ΔBHC vuông tại H có
\(\widehat{IBH}\) chung
Do đó: ΔBIH~ΔBHC
=>\(\dfrac{BI}{BH}=\dfrac{BH}{BC}\)
=>\(BH^2=BI\cdot BC\left(2\right)\)
Từ (1),(2) suy ra \(BK\cdot BA=BI\cdot BC\)
=>\(\dfrac{BK}{BC}=\dfrac{BI}{BA}\)
Xét ΔBKI vuông tại B và ΔBCA vuông tại B có
\(\dfrac{BK}{BC}=\dfrac{BI}{BA}\)
Do đó: ΔBKI~ΔBCA
e: ΔBCA vuông tại B
mà BM là đường trung tuyến
nên MB=MC
=>ΔMBC cân tại M
\(\widehat{NIB}+\widehat{NBI}=\widehat{MCB}+\widehat{MAB}=90^0\)
=>BM\(\perp\)IK tại N
ta có: \(BK\cdot BA=BH^2\)
=>\(BK\cdot15=12^2=144\)
=>BK=144/15=9,6(cm)
\(BI\cdot BC=BH^2\)
=>\(BI\cdot20=12^2=144\)
=>BI=7,2(cm)
Xét tứ giác BKHI có \(\widehat{BKH}=\widehat{BIH}=\widehat{KBI}=90^0\)
nên BKHI là hình chữ nhật
=>KI=BH=12(cm)
Xét ΔBIK vuông tại B có BN là đường cao
nên \(\left\{{}\begin{matrix}BN\cdot IK=BK\cdot BI\\KN\cdot KI=KB^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BN\cdot12=7,2\cdot9,6\\KN\cdot12=9,6^2\end{matrix}\right.\)
=>BN=5,76(cm); KN=7,68(cm)
ΔBKN vuông tại N
=>\(S_{BNK}=\dfrac{1}{2}\cdot NB\cdot NK=\dfrac{1}{2}\cdot5,76\cdot7,68=22,1184\left(cm^2\right)\)

\(\dfrac{3}{10}\left(giờ\right)=18\left(phút\right)\)
1/3 giờ=20 phút
2/5 giờ=24 phút
Vì 18<20<24<25
nên Quang đến trường trong thời gian ngắn nhất

a: Độ dài đáy bé là 220:2=110(m)
Chiều cao là \(\dfrac{1}{5}\left(220+110\right)=66\left(m\right)\)
Diện tích hình thang là:
\(\left(220+110\right)\times\dfrac{66}{2}=10890\left(m^2\right)=1,089\left(ha\right)\)
b: Khối lượng lúa thu được là:
10890:100x62=6751,8(kg)
a) Đáy bé của thửa ruộng dài:
\(220:2=110\left(m\right)\)
Chiều cao của thửa ruộng là:
\(220+110=330\left(m\right)\)
Diện tích thửa ruộng là:
\(\dfrac{\left(220+110\right)\cdot330}{2}=54450\left(m^2\right)=5,445\left(ha\right)\)
b) Số lúa thu được trên 1m2 là:
\(62:100=0,62\left(kg\right)\)
Số lúa thu được trên cả thửa ruộng là:
\(0,62\cdot54450=33759\left(kg\right)\)

11h40p thì kim giờ và kim phút sẽ nằm ở hai vị trí số 11 và số 8, cách nhau 3 số
=>Kim giờ và kim phút sẽ tạo ra góc 90 độ
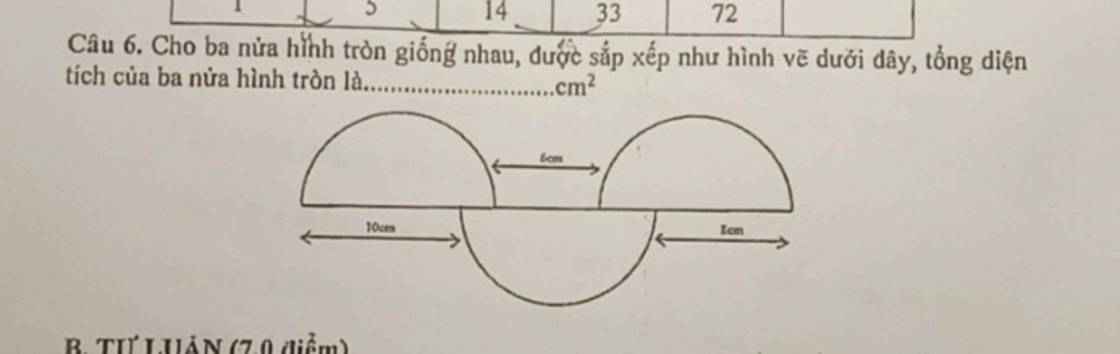
Lời giải:
Ký hiệu như hình vẽ:
Bán kính nửa đường tròn thứ nhất: $10+a$ (cm)
Bán kính nửa đường tròn số hai: $6+a+b$ (cm)
Bán kính nửa đường tròn thứ ba: $8+b$ (cm)
Vì 3 đường tròn này giống nhau nên:
$10+a=6+a+b$ và $6+a+b=8+b$
Với $10+a=6+a+b$
$\Rightarrow 10=6+b$
$b=10-6=4$ (cm)
Bán kính mỗi đường tròn: $8+b=8+4=12$ (cm)
Tổng diện tích 3 nửa đường tròn:
$12\times 12\times 3,14:2\times 3=678,24$ (cm2)