Chứng minh rằng nếu p là số nguyên tố lớn hơn 3 và 2p+1 cũng là số nguyên tố thì 4p+1 là hợp số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(x\in UC\left(1820;3080;4900\right)\left(40< x< 100\right)\)
\(1820=4.5.91=2^2.5.91\)
\(3080=40.77=2^3.5.7.11\)
\(4900=10^2.49=2^2.5^2.7^2\)
\(UCLN\left(1820;3080;4900\right)=2^2.5=20\)
\(\Rightarrow x\in UC\left(1820;3080;4900\right)=\left\{60;80\right\}\) Thỏa đề bài

a) 12 = 2².3
80 = 2⁴.5
56 = 2³.7
ƯCLN(12; 80; 56) = 2² = 4
b) 150 = 2.3.5²
50 = 2.5²
ƯCLN(150; 50) = 2.5² = 50
c) 1800 = 2³.3².5²
90 = 2.3².5
ƯCLN(1800; 90) = 2.3².5 = 90
d) 144 = 2⁴.3²
20 = 2².5
135 = 3³.5
ƯCLN(144; 20; 135) = 1
e) 24 = 2³.3
10 = 2.5
BCNN(24; 10) = 2³.3.5 = 120
f) 8 = 2³
12 = 2².3
15 = 3.5
BCNN(8; 12; 15) = 2³.3.5 = 120

\(320=8.40=2^3.2^2.2.5=2^6.5\)
\(1200=10^2.2^2.3=2^2.2^2.3.5^2=2^4.3.5^2\)
\(7500=10^2.5^2.3=2^2.5^2.5^2.3=2^2.5^4.3\)
320 = 26.5
1200 = 24.3.52
7500 = 22.3.54

Gọi số đối có thể lập được nhiều nhất là x (đội)
Ta có:
18 ⋮ x
27 ⋮ x
45 ⋮ x
=> x = ƯLCN(18;27;45)
ƯCLN(18;27;45) = 9
Vậy có thể chia nhiều nhất 9 đội
Mội đội sẽ có:
18 : 9 =2 (bác sĩ cấp cứu)
27 : 9 = 3 (bác sĩ đa khoa)
45 : 9 = 5 (điều dưỡng)
Số đội phản ứng nhanh nhiều nhất thỏa đề bài là :
\(UCLN\left(18;27;45\right)=3^2=9\left(đội\right)\)
Đáp số...


\(\dfrac{48}{96}-\dfrac{135}{270}\)
\(=\dfrac{48:48}{96:48}-\dfrac{135:135}{270:135}\)
\(=\dfrac{1}{2}-\dfrac{1}{2}\)
\(=0\)

Gọi x là số đội viên của liên đội \(\left(160< x< 190\right)\)
\(BCNN\left(3;4;5\right)=60\)
\(BC\left(3;4;5\right)=\left\{60;120;180;240;...\right\}\)
Theo đề bài \(x:\left(3;4;5\right)\) còn dư 2 và \(160< x< 190\)
\(\Rightarrow x\in\left[BC\left(3;4;5\right)+2\right]=180+2=182\)
Vậy số đội viên của liên đội là \(182\left(đội.viên\right)\)

a) \(A=1+2+2^2+...+2^{80}\)
\(2A=2+2^2+2^3+...+2^{81}\)
\(2A-A=2+2^2+2^3+...+2^{81}-1-2-2^2-...-2^{80}\)
\(A=2^{81}-1\)
Nên A + 1 là:
\(A+1=2^{81}-1+1=2^{81}\)
b) \(B=1+3+3^2+...+3^{99}\)
\(3B=3+3^2+3^3+...+3^{100}\)
\(3B-B=3+3^2+3^3+...+3^{100}-1-3-3^2-...-3^{99}\)
\(2B=3^{100}-1\)
Nên 2B + 1 là:
\(2B+1=3^{100}-1+1=3^{100}\)
2)
a) \(2^x\cdot\left(1+2+2^2+...+2^{2015}\right)+1=2^{2016}\)
Gọi:
\(A=1+2+2^2+...+2^{2015}\)
\(2A=2+2^2+2^3+...+2^{2016}\)
\(A=2^{2016}-1\)
Ta có:
\(2^x\cdot\left(2^{2016}-1\right)+1=2^{2016}\)
\(\Rightarrow2^x\cdot\left(2^{2016}-1\right)=2^{2016}-1\)
\(\Rightarrow2^x=\dfrac{2^{2016}-1}{2^{2016}-1}=1\)
\(\Rightarrow2^x=2^0\)
\(\Rightarrow x=0\)
b) \(8^x-1=1+2+2^2+...+2^{2015}\)
Gọi: \(B=1+2+2^2+...+2^{2015}\)
\(2B=2+2^2+2^3+...+2^{2016}\)
\(B=2^{2016}-1\)
Ta có:
\(8^x-1=2^{2016}-1\)
\(\Rightarrow\left(2^3\right)^x-1=2^{2016}-1\)
\(\Rightarrow2^{3x}-1=2^{2016}-1\)
\(\Rightarrow2^{3x}=2^{2016}\)
\(\Rightarrow3x=2016\)
\(\Rightarrow x=\dfrac{2016}{3}\)
\(\Rightarrow x=672\)
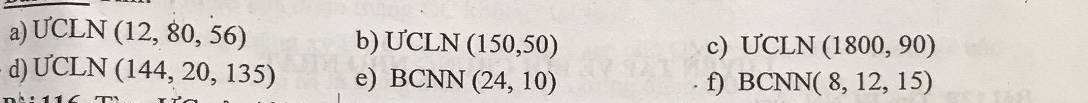
Vì p là số nguyên tố lớn hơn 3 nên \(p=3k+1\) hoặc \(p=3k+2\) \(\left(k\inℕ^∗\right)\)
Nếu \(p=k+1\) thì \(2p+1=2.\left(3k+1\right)+1=6k+3\in3\) và \(6k+3>3\)
\(\Leftrightarrow2p+1\) là hợp số \(\left(loại\right)\)
Nếu \(p=3k+2\) . Khi đó \(4p+1=4.\left(3k+2\right)=1=12k+9\in3\)
Và \(12k+9>3\) nên là hợp số \(\left(nhận\right)\)