5.(2⁵ - 10) : 2³

= 5.22 : 8

= 110 : 8

= 13,75

Cả 4 đáp án đều sai

\(5.\left(2^5-10\right):2^3\\ =5.\left(32-10\right):8\\ =5.22:8\\ =110:8\\ =13,75\)

Vậy không có đáp án nào đúng

a) n + 9 ⋮ n - 1

⇒ n - 1 + 10 ⋮ n - 1

⇒ 10 ⋮ n - 1

⇒ n - 1 ϵ Ư(10) = {1; -1; 2; -2; 5; -5; 10; -10} 

⇒ n ϵ {2; 0; 3; -1; 6; -4; 11; -9} 

b) n + 5 ⋮ 2n + 3 

⇒ 2(n + 5) ⋮ 2n + 3 

⇒ 2n + 10 ⋮ 2n + 3

⇒ 2n + 3 + 7 ⋮ 2n + 3

⇒ 7 ⋮ 2n + 3

⇒ 2n + 3 ϵ Ư(7) = {1; -1; 7; -7}

⇒ n ϵ {-1; -2; 2; -5} 

c) 2n + 4 ⋮ n + 6 

⇒ 2n + 12 - 8 ⋮ n + 6

⇒ 2(n + 6) - 8 ⋮ n + 6

⇒ 8 ⋮ n + 6

⇒ n + 6 ϵ Ư(8) = {1; -1; 2; -2; 4; -4; 8; -8}

⇒ n  ϵ {-5; -7; -4; -8; -2; -10; 2; -14} 

Với x = 2, ta có:

C = (4.2 - 6)/(2.2 + 1)

= 2/5 không phải số nguyên

Em xem lại đề nhé

\(C=\dfrac{4x-6}{2x+1}\\ =\dfrac{4x+2-8}{2x+1}\\ =\dfrac{2\left(2x+1\right)-8}{2x+1}\)

Ta có:

\(2\left(2x+1\right)⋮2x+1\)

Để \(\dfrac{4x-6}{2x+1}\inℤ\)

\(\rightarrow-8⋮2x+1\)

hay \(2x+1\inƯ\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)

Ta có bảng sau:

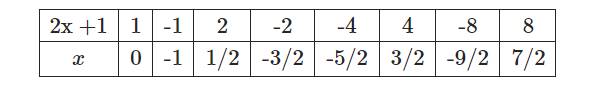
Vậy \(x\in\left\{0;-1;\dfrac{1}{2};-\dfrac{3}{2};-\dfrac{5}{2};\dfrac{3}{2};-\dfrac{9}{2};\dfrac{7}{2}\right\}\) thì \(\dfrac{4x-6}{2x+1}\inℤ\)

D = 3\(\dfrac{1}{2}\) \(\times\) \(\dfrac{12}{43}\) + \(\dfrac{49}{14}\) \(\times\) \(\dfrac{31}{43}\) + \(\dfrac{11}{2}\)

D = \(\dfrac{7}{2}\) \(\times\) \(\dfrac{12}{43}\) + \(\dfrac{7}{2}\)  \(\times\) \(\dfrac{31}{43}\) + \(\dfrac{11}{2}\)

D = \(\dfrac{7}{2\times43}\) \(\times\) (12 + 31) + \(\dfrac{11}{2}\)

D = \(\dfrac{7}{2\times43}\)  \(\times\) 43 + \(\dfrac{11}{2}\)

D = \(\dfrac{7}{2}\) + \(\dfrac{11}{2}\)

D = 9

D = 3 và 1/2 x 12/43 + 49/14 x 31/43 + 11/2
= 7/2 x 12/43 + 49/14 x 31/43 + 11/2
= 42/43 +  217/36 + 11/2
=9

# https://lazi.vn/user/tnsociu

A = 10¹.10².10³.10⁴...10⁸

A = 10^1+2+3+..+8

A = 10³⁶

A = 1.2 + 2.3 + 3.4 + 4.5 + ... + 99.100 + 100.101

3.A = 1.2.3 + 2.3.3 +3.4.3 + ... + 100.101.3

3A= 1.2.3 + 2.3.(4 - 1) + 3.4.(5 - 2) + ... + 100.101.(102 - 99)

3A = 1.2.3 + 2.3.4 - 1.2.3 + 2.3.4 -3.4.5 + ... +99.100.101 -100.101.102

3A = 99.100.101

A = 99.100.101 : 3

A = 33.100.101

Vậy A = 33. 100 .101 = 333300

{[(100+101)+100]+[(103.104.105 ):106 ].[(107 :108).109].1010}.1011=???

{[(1+10)+100]+[(1K.10K.100K):1M].[(10M:100M).1B].10B}.100B

K= nghìn

M= triệu

B= tỷ

\(\dfrac{123123}{456456}\) = \(\dfrac{123123:3003}{456456:3003}\) =  \(\dfrac{41}{152}\) = \(\dfrac{41.63}{152.63}\) = \(\dfrac{2583}{9576}\)

\(\dfrac{53}{504}\) = \(\dfrac{53.19}{504.19}\) = \(\dfrac{1007}{9576}\) 

\(\dfrac{123123}{456456}\)và\(\dfrac{53}{504}\)=\(\dfrac{62953992}{20053824}\)và\(\dfrac{24192168}{20053824}\)

Bài 1

a, cm : A = 16⁵ + 2¹⁵ ⋮ 3

    A = 16⁵ + 2¹⁵

   A = (2⁴)⁵ +  2¹⁵

  A  = 2²⁰ + 2¹⁵

 A  =  2¹⁵.(2⁵ + 1)

 A = 2¹⁵. 33 ⋮ 3 (đpcm)

b,cm : B = 8⁸ + 2²⁰ ⋮ 17

    B = (2³)⁸ + 2²⁰ 

    B =  2¹⁶ + 2²⁰

    B = 2¹⁶.(1 + 2⁴)

    B = 2¹⁶. 17 ⋮ 17 (đpcm)

c, cm: C = 1 - 2 + 2² - 2³ + 2⁴ - 2⁵ + 2⁶ -...-2²⁰²¹ + 2²⁰²² : 6 dư 1

C=1+(-2+2²-2³+2⁴- 2⁵+2⁶)+...+(-2²⁰¹⁷+2²⁰¹⁸-2²⁰¹⁹+2²⁰²⁰-2²⁰²¹+2²⁰²²)

C = 1 + 42 +...+ 2²⁰¹⁶.(-2 + 2² - 2³ + 2⁴ - 2⁵ + 2⁶)

C = 1 + 42+...+ 2²⁰¹⁶.42

C = 1 + 42.(2⁰+...+2²⁰¹⁶)

42 ⋮ 6 ⇒ C = 1 + 42.(2⁰+...+2²⁰¹⁶) : 6 dư 1 đpcm

Vì p là số nguyên tố lớn hơn 3 nên \(p=3k+1\) hoặc \(p=3k+2\) \(\left(k\inℕ^∗\right)\)

Nếu \(p=k+1\) thì \(2p+1=2.\left(3k+1\right)+1=6k+3\in3\) và \(6k+3>3\)

\(\Leftrightarrow2p+1\) là hợp số \(\left(loại\right)\)

Nếu \(p=3k+2\) . Khi đó \(4p+1=4.\left(3k+2\right)=1=12k+9\in3\)

Và \(12k+9>3\) nên là hợp số \(\left(nhận\right)\)

Đặt \(x\in UC\left(1820;3080;4900\right)\left(40< x< 100\right)\)

\(1820=4.5.91=2^2.5.91\)

\(3080=40.77=2^3.5.7.11\)

\(4900=10^2.49=2^2.5^2.7^2\)

\(UCLN\left(1820;3080;4900\right)=2^2.5=20\)

\(\Rightarrow x\in UC\left(1820;3080;4900\right)=\left\{60;80\right\}\) Thỏa đề bài