Một người đi xe đạp đi từ A đến B với vận tốc 16km/giờ. Người đó khởi hành lúc 6 giờ 45 phút và đến B lúc 9 giờ 30 phút. Tính độ dài quãng đường AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
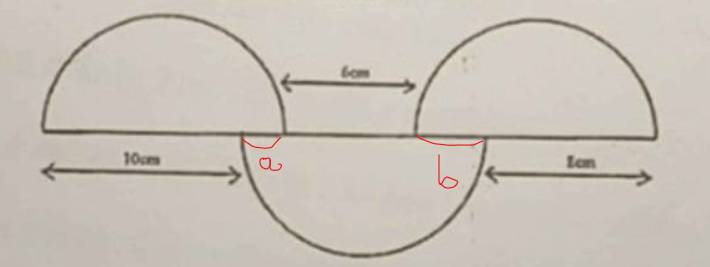
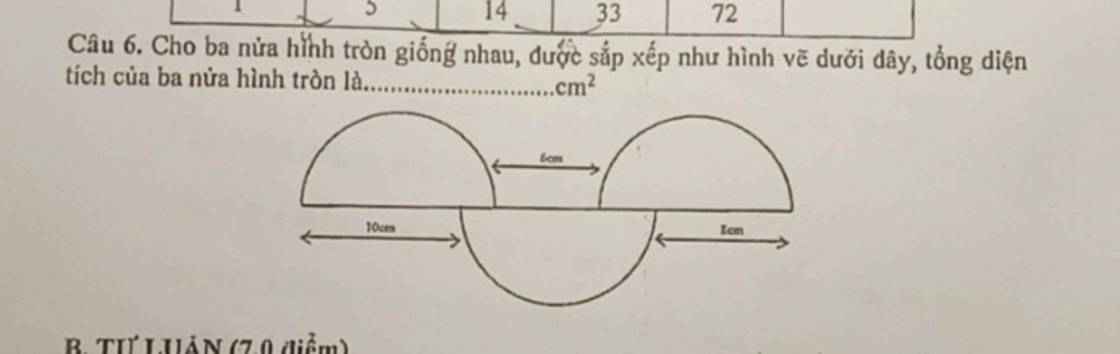
Ký hiệu như hình vẽ:
Bán kính nửa đường tròn thứ nhất: $10+a$ (cm)
Bán kính nửa đường tròn số hai: $6+a+b$ (cm)
Bán kính nửa đường tròn thứ ba: $8+b$ (cm)
Vì 3 đường tròn này giống nhau nên:
$10+a=6+a+b$ và $6+a+b=8+b$
Với $10+a=6+a+b$
$\Rightarrow 10=6+b$
$b=10-6=4$ (cm)
Bán kính mỗi đường tròn: $8+b=8+4=12$ (cm)
Tổng diện tích 3 nửa đường tròn:
$12\times 12\times 3,14:2\times 3=678,24$ (cm2)

a: Xét ΔCHB vuông tại H và ΔCBA vuông tại B có
\(\widehat{HCB}\) chung
Do đó: ΔCHB~ΔCBA
b:
Xét ΔAHB vuông tại H và ΔABC vuông tại B có
\(\widehat{HAB}\) chung
Do đó: ΔAHB~ΔABC
=>\(\dfrac{AH}{AB}=\dfrac{AB}{AC}\)
=>\(AB^2=AH\cdot AC\)
c: ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(AC=\sqrt{15^2+20^2}=25\left(cm\right)\)
ΔAHB~ΔABC
=>\(\dfrac{BH}{BC}=\dfrac{BA}{AC}\)
=>\(BH=\dfrac{AB\cdot BC}{AC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
d: Xét ΔBKH vuông tại K và ΔBHA vuông tại H có
\(\widehat{KBH}\) chung
Do đó: ΔBKH~ΔBHA
=>\(\dfrac{BK}{BH}=\dfrac{BH}{BA}\)
=>\(BH^2=BK\cdot BA\left(1\right)\)
Xét ΔBIH vuông tại I và ΔBHC vuông tại H có
\(\widehat{IBH}\) chung
Do đó: ΔBIH~ΔBHC
=>\(\dfrac{BI}{BH}=\dfrac{BH}{BC}\)
=>\(BH^2=BI\cdot BC\left(2\right)\)
Từ (1),(2) suy ra \(BK\cdot BA=BI\cdot BC\)
=>\(\dfrac{BK}{BC}=\dfrac{BI}{BA}\)
Xét ΔBKI vuông tại B và ΔBCA vuông tại B có
\(\dfrac{BK}{BC}=\dfrac{BI}{BA}\)
Do đó: ΔBKI~ΔBCA
e: ΔBCA vuông tại B
mà BM là đường trung tuyến
nên MB=MC
=>ΔMBC cân tại M
\(\widehat{NIB}+\widehat{NBI}=\widehat{MCB}+\widehat{MAB}=90^0\)
=>BM\(\perp\)IK tại N
ta có: \(BK\cdot BA=BH^2\)
=>\(BK\cdot15=12^2=144\)
=>BK=144/15=9,6(cm)
\(BI\cdot BC=BH^2\)
=>\(BI\cdot20=12^2=144\)
=>BI=7,2(cm)
Xét tứ giác BKHI có \(\widehat{BKH}=\widehat{BIH}=\widehat{KBI}=90^0\)
nên BKHI là hình chữ nhật
=>KI=BH=12(cm)
Xét ΔBIK vuông tại B có BN là đường cao
nên \(\left\{{}\begin{matrix}BN\cdot IK=BK\cdot BI\\KN\cdot KI=KB^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BN\cdot12=7,2\cdot9,6\\KN\cdot12=9,6^2\end{matrix}\right.\)
=>BN=5,76(cm); KN=7,68(cm)
ΔBKN vuông tại N
=>\(S_{BNK}=\dfrac{1}{2}\cdot NB\cdot NK=\dfrac{1}{2}\cdot5,76\cdot7,68=22,1184\left(cm^2\right)\)

\(\dfrac{3}{10}\left(giờ\right)=18\left(phút\right)\)
1/3 giờ=20 phút
2/5 giờ=24 phút
Vì 18<20<24<25
nên Quang đến trường trong thời gian ngắn nhất

a: Độ dài đáy bé là 220:2=110(m)
Chiều cao là \(\dfrac{1}{5}\left(220+110\right)=66\left(m\right)\)
Diện tích hình thang là:
\(\left(220+110\right)\times\dfrac{66}{2}=10890\left(m^2\right)=1,089\left(ha\right)\)
b: Khối lượng lúa thu được là:
10890:100x62=6751,8(kg)
a) Đáy bé của thửa ruộng dài:
\(220:2=110\left(m\right)\)
Chiều cao của thửa ruộng là:
\(220+110=330\left(m\right)\)
Diện tích thửa ruộng là:
\(\dfrac{\left(220+110\right)\cdot330}{2}=54450\left(m^2\right)=5,445\left(ha\right)\)
b) Số lúa thu được trên 1m2 là:
\(62:100=0,62\left(kg\right)\)
Số lúa thu được trên cả thửa ruộng là:
\(0,62\cdot54450=33759\left(kg\right)\)

11h40p thì kim giờ và kim phút sẽ nằm ở hai vị trí số 11 và số 8, cách nhau 3 số
=>Kim giờ và kim phút sẽ tạo ra góc 90 độ
Thời gian người đó đi hết quãng đường AB là:
9h30p-6h45p=2h45p=2,75(giờ)
Độ dài quãng đường AB là:
16x2,75=44(km)