Tìm tổng sau
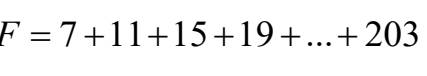
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Số phần tử:
\(\left(9-2\right):1+1=8\) (phần tử)
b) Số phần tử:
\(\left(20-2\right):2+1=10\) (phẩn tử)
c) Số phần tử:
\(\left(25-1\right):3+1=9\) (phần tử)
d) Số phần tử:
\(\left(104-2\right):2+1=52\) (phần tử)
e) Số phần tử:
\(\left(470-5\right):5+1=94\) (phần tử)
f) Số phần tử:
\(\left(500-10\right):10+1=50\) (phần tử)

Gọi số học sinh của trường đó là x (học sinh)
Vì khi xếp x học sinh thành 20; 25 hoặc 30 hàng đều dư 15 học sinh nên khi xếp (x - 15) học sinh thành 20; 25 hoặc 30 hàng thì vừa đủ.
Do đó ta có \(\left(x-15\right)⋮20;25;30\) và \(x⋮41\)
Mà BCNN(20; 25; 30) = 300 nên ta cũng có thể viết \(\left(x-15\right)⋮300\).
Ta có \(\left(x-15\right)\in\left\{300;600;900\right\}\), suy ra \(x\in\left\{315;615;915\right\}\).
Thử chia các giá trị trên cho 41 chỉ có 615 chia hết cho 41, thỏa mãn đề bài.
Vậy số học sinh của trường đó là 615 học sinh.


Ta có:
\(A=2^2+2^3+2^4+...+2^{99}\)
\(A=\left(2^2+2^3\right)+\left(2^4+2^5\right)+...+\left(2^{98}+2^{99}\right)\)
\(A=12+2^2.\left(2^2+2^3\right)+...+2^{96}.\left(2^2+2^3\right)\)
\(A=12+2^2.12+...+2^{96}.12\)
\(A=12.\left(1+2^2+...+2^{96}\right)\)
Vì \(12⋮3\) nên \(12.\left(1+2^2+...+2^{96}\right)⋮3\)
Vậy \(A⋮3\)

e) \(2^x+2^{x+3}=144\)
\(=>2^x+2^x.2^3=144\)
\(=>2^x.\left(1+2^3\right)=144\)
\(=>2^x.9=144\)
\(=>2^x=144:9\)
\(=>2^x=16=2^4\)
\(=>x=4\)
__________
f) \(3^x+3^{x+1}=108\)
\(=>3^x+3^x.3=108\)
\(=>3^x.\left(1+3\right)=108\)
\(=>3^x.4=108\)
\(=>3^x=108:4\)
\(=>3^x=27=3^3\)
\(=>x=3\)
\(#Wendy.Dang\)

a) Vì \(n;n+1\) là 2 số tự nhiên liên tiếp \(\left(n< n+1\right)\)
\(\Rightarrow\left(n;n+1\right)=1\)
\(\Rightarrow UCLN\left(n;n+1\right)=1\)
b) \(4n+18=2\left(2n+9\right)⋮\left(1;2;2n+9\right)\left(n\inℕ\right)\)
Ta lại có :
\(2n+9⋮2n+1\)
\(\Leftrightarrow2n+9-2n-1⋮2n+1\)
\(\Leftrightarrow8⋮2n+1\)
\(\Leftrightarrow2n+1\in\left\{1;2;4;8\right\}\)
\(\Leftrightarrow n\in\left\{0\right\}\)
\(\Rightarrow UCLN\left(2n+1;4n+18\right)=UCLN\left(1;18\right)=1\left(n=0\right)\)
\(\Rightarrow\left(2n+1;2n+9\right)=1\)
mà \(2n+1⋮\left(1;2n+1\right)\)
\(\Rightarrow UCLN\left(2n+1;4n+18\right)=1\)

Hai số tự nhiên lẻ là \(n+1;n+3\left(n\inℕ\right)\)
Tổng của chúng là :
\(n+1+n+3=2n+4=2\left(n+2\right)⋮\left(2;n+2\right)\)
\(\Rightarrow dpcm\)

a) 4915 = 4914.49 = (492)7.49 = (2 401)7.49
Vì (2 401)7 có chữ số tận cùng là 1 nên (2 401)7.49 có chữ số tận cùng là 9.
Vậy chữ số tận cùng của số 4915 là 9.
b) Ta có: \(54^{10}=\left(54^2\right)^5=2916^5\)
Tích của 5 chữ số 6 có chữ số tận cùng là 6 nên \(2916^5\) có chữ số tận cùng là 6.
Vậy \(54^{10}\) có chữ số tận cùng là 6.
c) Ta có 1120 có chữ số tận cùng là 1;
11921 có chữ số tận cùng là 9;
2 00022 có chữ số tận cùng là 0.
Khi đó 1120 + 11921 + 2 00022 có chữ số tận cùng là chữ số tận cùng của tổng 1 + 9 + 0 =10.
Vậy 1120 + 11921 + 2 00022 có chữ số tận cùng là 0.
F = 7 + 11 + 15 + 19 +...+ 203
Dãy số trên là dãy số cách đều với khoảng cách là: 11 - 7 = 4
Số số hạng của dãy số trên là: (203 - 7): 4 + 1 = 50
Tổng F là: (203 + 7) x 50: 2 = 5250