C = 1/(sqrt(x) + 2) + 1/(sqrt(x) - 2) + 4/(x - 4) với x >= 0 và x ≠4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2-\left(2m+1\right)x+m^2+1=0\)
\(\text{Δ}=\left(2m+1\right)^2-4\cdot1\cdot\left(m^2+1\right)\)
\(=4m^2+4m+1-4m^2-4=4m-3\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>4m-3>0
=>4m>3
=>\(m>\dfrac{3}{4}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+1\\x_1x_2=\dfrac{c}{a}=m^2+1\end{matrix}\right.\)
\(A=\left(2x_1-x_2\right)\left(x_1-2x_2\right)\)
\(=2x_1^2+2x_2^2-5x_1x_2\)
\(=2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-5x_1x_2\)
\(=2\left[\left(2m+1\right)^2-2\left(m^2+1\right)\right]-5\left(m^2+1\right)\)
\(=2\left(2m+1\right)^2-9\left(m^2+1\right)\)
\(=2\left(4m^2+4m+1\right)-9m^2-9\)
\(=8m^2+8m+2-9m^2-9\)
\(=-m^2+8m-7\)
\(=-\left(m^2-8m+7\right)\)
\(=-\left(m^2-8m+16-9\right)\)
\(=-\left(m-4\right)^2+9< =9\forall m\)
Dấu '=' xảy ra khi m=4

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
\(\left|P\right|+P=0\)
=>|P|=-P
=>P<=0
=>\(\dfrac{3\sqrt{x}}{\sqrt{x}-3}< =0\)
=>\(\dfrac{\sqrt{x}}{\sqrt{x}-3}< =0\)
=>\(0< =\sqrt{x}< 3\)
=>\(0< =x< 9\)

Để hệ có nghiệm duy nhất thì \(\dfrac{1}{m}\ne\dfrac{m}{1}\)
=>\(m^2\ne1\)
=>\(m\notin\left\{1;-1\right\}\)
Sửa đề: \(\left\{{}\begin{matrix}x+my=m+1\\mx+y=2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}mx+m^2y=m^2+m\\mx+y=2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y\left(m^2-1\right)=m^2-m\\x+my=m+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m\left(m-1\right)}{\left(m-1\right)\left(m+1\right)}=\dfrac{m}{m+1}\\x=m+1-my=m+1-\dfrac{m^2}{m+1}=\dfrac{2m+1}{m+1}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x>=2\\y>=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2m+1-2m-2}{m+1}>=0\\\dfrac{m-m-1}{m+1}>=0\end{matrix}\right.\)
=>\(-\dfrac{1}{m+1}>=0\)
=>m+1<0
=>m<-1
mà \(m\in\left(-10;10\right)\)
nên \(m\in\left\{-9;-8;...;-2\right\}\)
=>Có 8 số nguyên m thỏa mãn

a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
b: Ta có; ΔOCD cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)CD tại K
Ta có: \(\widehat{OKM}=\widehat{OAM}=\widehat{OBM}=90^0\)
=>O,K,A,M,B cùng thuộc đường tròn đường kính OM
c: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(2)
Từ (1),(2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H
Xét ΔOHN vuông tại H và ΔOKM vuông tại K có
\(\widehat{HON}\) chung
Do đó: ΔOHN~ΔOKM
=>\(\dfrac{OH}{OK}=\dfrac{ON}{OM}\)
=>\(OH\cdot OM=OK\cdot ON\left(3\right)\)
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2=R^2\left(4\right)\)
Từ (3),(4) suy ra \(OK\cdot ON=R^2=OD^2\)
=>\(\dfrac{OK}{OD}=\dfrac{OD}{ON}\)
Xét ΔOKD và ΔODN có
\(\dfrac{OK}{OD}=\dfrac{OD}{ON}\)
\(\widehat{KOD}\) chung
Do đó: ΔOKD~ΔODN
=>\(\widehat{OKD}=\widehat{ODN}=90^0\)
=>ND là tiếp tuyến của (O)

Để tìm giá trị lớn nhất của biểu thức \( P \), ta sẽ sử dụng bất đẳng thức Cauchy-Schwarz (hay bất đẳng thức Buniakovskii):
Đặt \( x = \sqrt{a}, y = \sqrt{b}, z = \sqrt{c} \), ta có \( a = x^2, b = y^2, c = z^2 \).
Biểu thức \( P \) sẽ trở thành:
\[ P = \frac{x^2}{x^2+3} + \frac{y^2}{y^2+3} + \frac{z^2}{z^2+3} + \frac{xy}{3x+z} + \frac{yz}{3y+x} + \frac{zx}{3z+y} \]
Sử dụng bất đẳng thức Cauchy-Schwarz, ta có:
\[ P \geq \frac{(x+y+z)^2}{x^2+y^2+z^2+3(x+y+z)} + \frac{(xy+yz+zx)^2}{3(xy+yz+zx)+xy(x+y+z)} \]
Do \( x+y+z = \sqrt{a} + \sqrt{b} + \sqrt{c} \leq \sqrt{3(a+b+c)} = 3 \), và \( xy+yz+zx \leq \frac{(x+y+z)^2}{3} \), ta có:
\[ P \geq \frac{9}{9+9} + \frac{\frac{(x+y+z)^2}{9}}{3 \times \frac{(x+y+z)^2}{9} + \frac{(x+y+z)^3}{27}} \]
\[ = \frac{1}{2} + \frac{1}{3+\frac{1}{3}} \]
\[ = \frac{1}{2} + \frac{1}{\frac{10}{3}} \]
\[ = \frac{1}{2} + \frac{3}{10} \]
\[ = \frac{8}{10} = \frac{4}{5} \]
Vậy, giá trị lớn nhất của \( P \) là \( \frac{4}{5} \), đạt được khi \( a = b = c = 1 \).

a) Với m = 1, ta có:
⇒ (d): y = x - 1/2 + 2 = x + 3/2
Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = x + 3/2
⇔ x² = 2x + 3
⇔ x² - 2x - 3 = 0
Do a - b + c = 1 - (-2) + 3 = 0 nên phương trình có hai nghiệm:
x₁ = -1; x₂ = -c/a = 3
x₁ = -1 ⇒ y = 1/2 . (-1)² = 1/2
⇒ A(-1; 1/2)
x₂ = 3 ⇒ y = 1/2 . 3² = 9/2
⇒ B(3; 9/2)
b) Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = mx - 1/2 m² + m + 1
⇔ x² = 2mx - m² + 2m + 2
⇔ x² - 2mx + m² - 2m - 2
∆' = (-m)² - 1.(m² - 2m - 2)
= m² - m² + 2m + 2
= 2m + 2
Để phương trình có hai nghiệm phân biệt thì ∆' > 0
⇔ 2m + 2 > 0
⇔ 2m > -2
⇔ m > -1
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = 2m
x₁x₂ = m² - 2m - 2
Ta có:
|x₁ - x₂| = (x₁ - x₂)² = [(x₁ + x₂)² - 4x₁x₂]
= [(2m)² - 4.(m² - 2m - 2)]
= (4m² - 4m² + 8m + 4)
= 8m + 4
= 2(2m + 2)
Mà |x₁ - x₂| = 2
⇔ 2(2m + 2) = 2
⇔ (2m + 2) = 1
⇔ 2m + 2 = 1
⇔ 2m = -1
⇔ m = -1/2 (nhận)
Vậy m = -1/2 thì phương trình có hai nghiệm phân biệt thỏa mãn |x₁ - x₂| = 2
 cho a,b,c là độ dài 3 cạnh tam giác có chu vi bằng 4
cho a,b,c là độ dài 3 cạnh tam giác có chu vi bằng 4
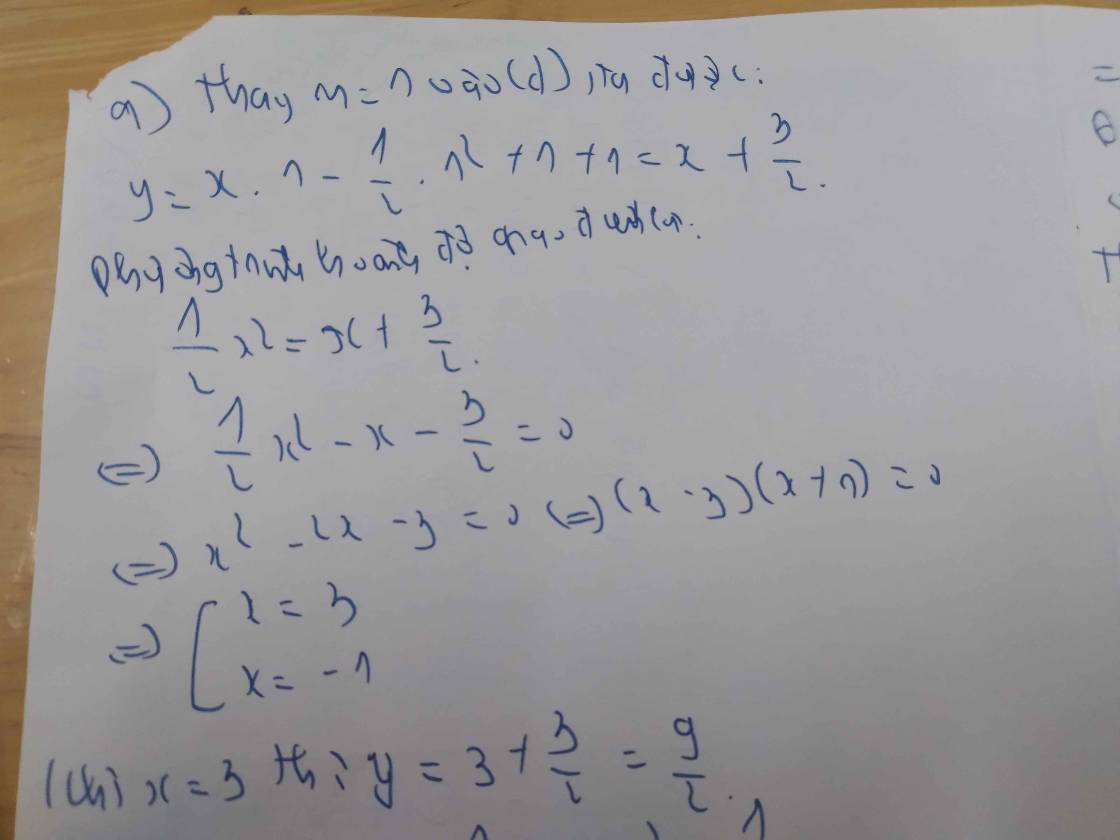


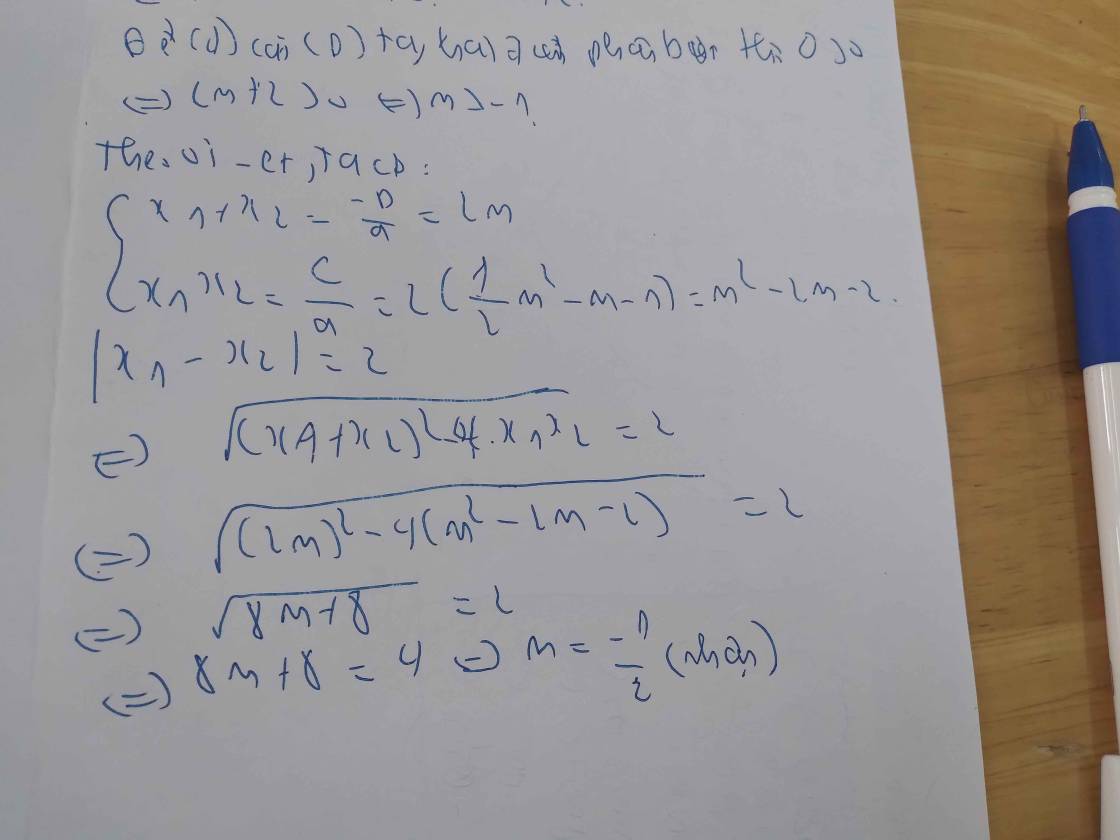
\(C=\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}+\dfrac{4}{x-4};\left(x\ge0;x\ne4\right)\)
\(=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2}{\sqrt{x}-2}\)
bgngnbvvbvcnnnbbbbbbbbbbbbb