lay day can 5 l do nuoc trong can 5 l vao day can 3l do nuoc trong can 3l di do tiep 2 l trong can 5l vao can 3l lay day can 5l lam tuong tu nhu vay ta con 1l trong can 5 l do la luong nuoc ta can

Ta lấy đầy cả hai can

Ta đổ số nước ở can 5l , số nước đó = 3l ( số nước đổ = số lít nước ở can 3l )

Sau đó chia đôi số nước là xong

Bước 1: Lấy 5 lít từ bể nước vào can 5 lít rồi đổ vào can 3 lít đến khi can 3 lít đầy thì thôi. Trong can 5 lít lúc này chứa 2 lít nước

Bước 2: Đổ nước từ can 3 lít xuống bể, rồi lấy can 5 lít đổ 2 lít vào can 3 lít. Trong can 3 lít lúc này chứa 2 lít nước.

Bước 3 : Lấy 5 lít từ bể vào can 5 lít. Đổ cho đầy can 3 lít. Trong can 5 lít lúc này chứa lít nước

Bước 4: Đổ nước từ can 3 lít xuống bể. Lấy can 5 lít đẩy vào can 3 lít cho đầy can 3 lít thì trong can 5 lít sẽ còn 1 lít nước.

làm giống thành ấy

a: ΔABC vuông tại A

=>ΔABC nội tiếp đường tròn đường kính BC

Tâm O là trung điểm của BC

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{7^2+24^2}=25\left(cm\right)\)

Bán kính là \(R=\dfrac{BC}{2}=\dfrac{25}{2}=12,5\left(cm\right)\)

b: Chu vi tam giác MNP là:

\(C=2a\sqrt{3}+2a\sqrt{3}+2a\sqrt{3}=6a\sqrt{3}\)

Diện tích tam giác MNP là:

\(S=\dfrac{MN^2\cdot\sqrt{3}}{4}=\left(2a\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{4a^2\cdot3\cdot\sqrt{3}}{4}=3a^2\sqrt{3}\)

\(S=p\cdot r\)

=>\(r=\dfrac{S}{p}=\dfrac{3a^2\sqrt{3}}{\dfrac{C}{2}}=\dfrac{3a^2\sqrt{3}}{3a\sqrt{3}}=a\)

Xét ΔMNP có \(\dfrac{BC}{sinA}=2R\)

=>\(2R=\dfrac{2a\sqrt{3}}{sin60}=2a\sqrt{3}:\dfrac{\sqrt{3}}{2}=2a\sqrt{3}\cdot\dfrac{2}{\sqrt{3}}=4a\)

=>R=2a

a: ΔABC vuông tại A

=>ΔABC nội tiếp đường tròn đường kính BC

Tâm O là trung điểm của BC

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{7^2+24^2}=25\left(cm\right)\)

Bán kính là \(R=\dfrac{BC}{2}=\dfrac{25}{2}=12,5\left(cm\right)\)

b: Chu vi tam giác MNP là:

\(C=2a\sqrt{3}+2a\sqrt{3}+2a\sqrt{3}=6a\sqrt{3}\)

Diện tích tam giác MNP là:

\(S=\dfrac{MN^2\cdot\sqrt{3}}{4}=\left(2a\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{4a^2\cdot3\cdot\sqrt{3}}{4}=3a^2\sqrt{3}\)

\(S=p\cdot r\)

=>\(r=\dfrac{S}{p}=\dfrac{3a^2\sqrt{3}}{\dfrac{C}{2}}=\dfrac{3a^2\sqrt{3}}{3a\sqrt{3}}=a\)

Xét ΔMNP có \(\dfrac{BC}{sinA}=2R\)

=>\(2R=\dfrac{2a\sqrt{3}}{sin60}=2a\sqrt{3}:\dfrac{\sqrt{3}}{2}=2a\sqrt{3}\cdot\dfrac{2}{\sqrt{3}}=4a\)

=>R=2a

Xét (O) có \(\widehat{BAC}\) là góc nội tiếp chắn cung BC

nên \(\widehat{BAC}=\dfrac{\widehat{BOC}}{2}=\dfrac{110^0}{2}=55^0\)

ΔBAC cân tại A

=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-\widehat{BAC}}{2}=\dfrac{180^0-55^0}{2}=\dfrac{125^0}{2}=62,5^0\)

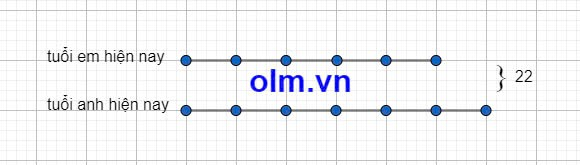
Tổng số tuổi của hai người là 11x2=22(tuổi)

Tỉ số giữa tuổi anh và tuổi em là:

\(\dfrac{4}{5}:\dfrac{2}{3}=\dfrac{4}{5}\times\dfrac{3}{2}=\dfrac{12}{10}=\dfrac{6}{5}\)

Tuổi anh hiện nay là \(22:\left(6+5\right)\times6=22:11\times6=12\left(tuổi\right)\)

Tuổi em hiện nay là 22-12=10(tuổi)

Tuổi anh sau đây 3 năm nữa là 12+3=15(tuổi)

Tuổi em sau đây 3 năm nữa là 10+3=13(tuổi)

Bổ sung sơ đồ đoạn thẳng:

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC=\sqrt{4^2-2^2}=2\sqrt{3}\left(cm\right)\)

Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC}=\dfrac{1}{2}\)

nên \(\widehat{B}=60^0\)

Ta có: \(65\cdot\left(35-9\right)-35\left(65+9\right)\)

\(=65\cdot35-65\cdot9-65\cdot35-35\cdot9\)

\(=-65\cdot9-35\cdot9\)

\(=-9\left(65+35\right)=-9\cdot100=-900\)

a: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)

nên BEDC là tứ giác nội tiếp

=>B,E,D,C cùng thuộc một đường tròn

b: Xét (B;BD) có

BD là bán kính

AC\(\perp\)BD tại D

Do đó: AC là tiếp tuyến của (B;BD)

a: Xét (O) có \(\widehat{BAC}\) là góc nội tiếp chắn cung BC

nên \(\widehat{BAC}=\dfrac{1}{2}\cdot\widehat{BOC}\)

Xét ΔOBC có OB=OC

nên ΔOBC cân tại O

=>\(\widehat{OBC}=\dfrac{180^0-\widehat{BOC}}{2}=90^0-\widehat{BAC}\)

b: H là trực tâm của ΔABC

=>AH\(\perp\)BC

=>\(\widehat{BAH}=90^0-\widehat{ABC}\left(1\right)\)

Xét ΔOAC có OA=OC

nên ΔOAC cân tại O

=>\(\widehat{OAC}=\dfrac{180^0-\widehat{AOC}}{2}=90^0-\dfrac{1}{2}\cdot\widehat{AOC}=90^0-\widehat{ABC}\left(2\right)\)

Từ (1),(2) suy ra \(\widehat{BAH}=\widehat{OAC}\)

a: Xét (O) có

\(\widehat{ABC};\widehat{ADC}\) là các góc nội tiếp chắn cung AC

nên \(\widehat{ABC}=\widehat{ADC}\)

Xét (O) có

ΔACD nội tiếp

AD là đường kính

Do đó: ΔACD vuông tại C

Xét ΔAHB vuông tại H và ΔACD vuông tại C có

\(\widehat{ABH}=\widehat{ADC}\)

Do đó: ΔAHB~ΔACD

b: ΔAHB~ΔACD

=>\(\dfrac{AH}{AC}=\dfrac{AB}{AD}\)

=>\(AD=\dfrac{AB\cdot AC}{AH}=\dfrac{8\cdot15}{5}=8\cdot3=24\left(cm\right)\)

Bán kính của (O) là 24:2=12(cm)