Tìm các số nguyên tố p sao cho p + 8 và 4p + 1 đều là các số nguyên tố.
Ai giúp mình với, mình đang cần gấp!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

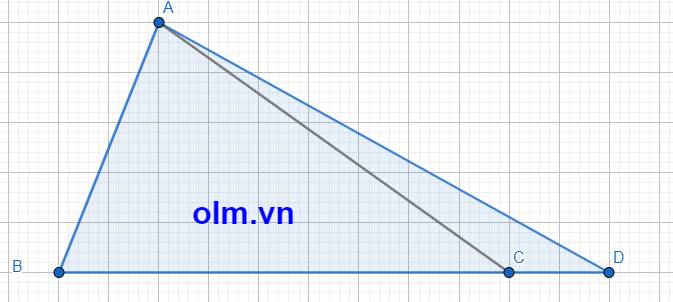
BD = BC + CD = BC + \(\dfrac{2}{9}\)BC = \(\dfrac{11}{9}\)BC
SABD = \(\dfrac{11}{9}\)SABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BD = \(\dfrac{11}{9}\)BC)
Diện tích tam giác ABD là:
351 \(\times\) \(\dfrac{11}{9}\) = 429 (cm2)
Đáp số: 429 (cm2)


Cho dãy số: ...;146; 150; 154
Dãy số trên là dãy số cách đều với khoảng cách là: 150 - 146 = 4
Số đầu tiên của dãy số trên là: 154 - 4\(\times\)(25 -1) = 58
Đáp số: 58

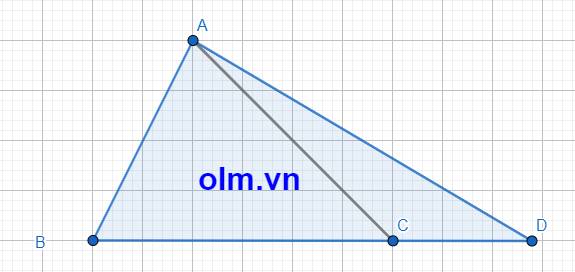
CD = BC + CD = BC + \(\dfrac{6}{13}\)BC = \(\dfrac{19}{13}\)BC
SABD = \(\dfrac{19}{13}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và AD = \(\dfrac{19}{13}\)BC)
Diện tích tam giác ABD là: 481 \(\times\)\(\dfrac{19}{13}\) = 703(cm2)
Đáp số: 703 cm2

a) Theo đề f(x) nhận -2 là nghiệm lấy -2 thay vào x ta có:
\(\left(-2\right)^2-2m+2=0\)
\(\Rightarrow4-2m+2=0\)
\(\Rightarrow6-2m=0\)
\(\Rightarrow2m=6\)
\(\Rightarrow m=3\)
b) Tìm được m ta có: \(f\left(x\right)=x^2+3x+2\)
\(\Rightarrow x^2+3x+2=0\)
\(\Rightarrow x^2+2x+x+2=0\)
\(\Rightarrow x\left(x+2\right)+\left(x+2\right)=0\)
\(\Rightarrow\left(x+2\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=-1\end{matrix}\right.\)
Vậy tập nghiệm của f(x) là: \(S=\left\{-2;-1\right\}\)

`@` `\text {Ans}`
`\downarrow`
`4,`
`a)`
\(f(x)=x(1-2x) + (2x^2 -x +4 )=0\)
`=> x-2x^2 + 2x^2-x+4=0`
`=> (x-x)+(-2x^2+2x^2)+4=0`
`=> 4=0 (\text {vô lí})`
Vậy, đa thức không có nghiệm.
`b)`
\(g(x) = x(x-5) - x(x+2)+ 7x=0\)
`=> x^2-5x-x^2-2x+7x=0`
`=> (x^2-x^2)+(-5x-2x+7x)=0`
`=> 0=0 (\text {luôn đúng})`
Vậy, đa thức có vô số nghiệm.
`c)`
\(h(x)= x(x-1) +1=0\)
`=> x^2-x+1=0`
Vì \(x^2 \ge 0\) \(\forall\) `x`
`=> x^2 - x + 1 \ge 1`\(\forall x\)
`1 \ne 0`
`=>` Đa thức vô nghiệm.
`\text {#KaizuulvG}`

Vì số đó chia 3 dư 1 và chia 4 dư 3 nên khi số đó thêm vào 17 đơn vị thì ta sẽ được số mới chia hết cho cả 3 và 4.
Vì số đó chia 4 dư 3 nên số đó phải lớn hơn hoặc cùng lắm là bằng 3.
vậy số mới lúc sau phải lớn hơn hoặc cùng lắm là bằng 17 + 3 = 20
Số nhỏ nhất lớn 20 mà chia hết cho 12 là 24
Vậy số cần là 24 - 17 = 7
Đáp số: 7

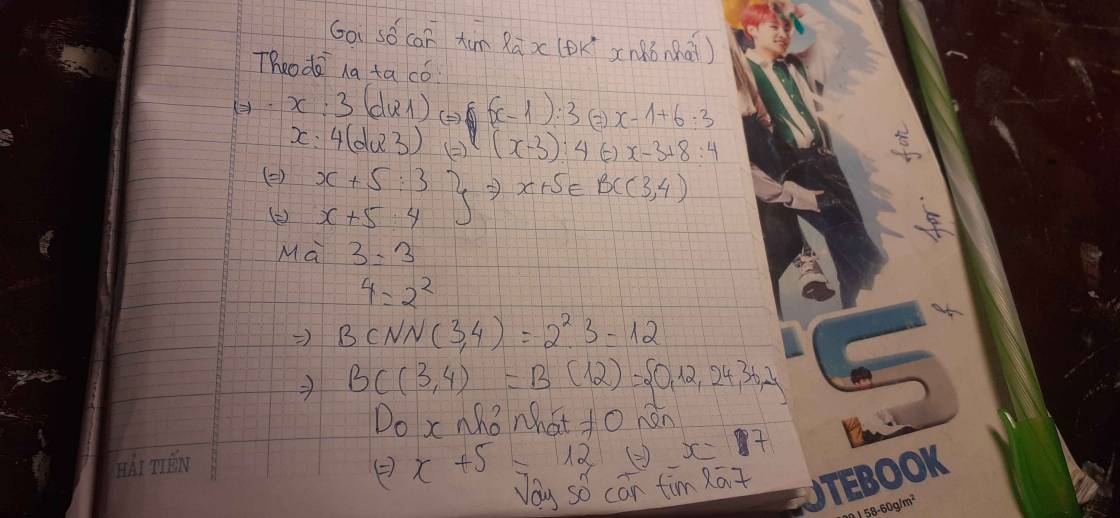
Giải bằng phương pháp đánh giá em nhé.
+ Nếu p = 2 ta có:
2 + 8 = 10 (loại)
+ Nếu p = 3 ta có:
3 + 8 = 11 (nhận)
4.3 + 1 = 13 (nhận)
+ Nếu p = 3\(k\) + 1 ta có:
p + 8 = 3\(k\) + 1 + 8 = 3\(k\) + 9 = 3(\(k+3\)) là hợp số (loại)
+ nếu p = 3\(k\) + 2 ta có:
4p + 1 = 4(3\(k\) + 2) + 1 = 12\(k\) + 9 = 3\(\left(4k+3\right)\) là hợp số loại
Vậy p = 3 là giá trị thỏa mãn đề bài
Kết luận: số nguyên tố p sao cho p + 8 và 4p + 1 đều là các số nguyên tố đó là 3