kb với miinhf ko

a) Ta thấy \(\dfrac{EA}{EK}=\dfrac{ED}{EB}=\dfrac{EG}{EA}\) nên \(AE^2=EK.EG\) (đpcm)

b) Ta có \(\dfrac{AE}{AK}+\dfrac{AE}{AG}=\dfrac{DE}{DB}+\dfrac{BE}{BD}=\dfrac{DE+BE}{BD}=1\) nên suy ra \(\dfrac{1}{AE}=\dfrac{1}{AK}+\dfrac{1}{AG}\) (đpcm)

Bài 1:

a, (3\(x\) + 2)(4\(x\) - 1) - (2\(x\) - 1)(6\(x\) - 5)

 = 12\(x^2\) - 3\(x\) + 8\(x\) - 2 - 12\(x^2\)  + 10\(x\) + 6\(x\) - 5

 = 21\(x\) - 7

b, (2\(x\) + 1)(\(x^2\) - 7y) - 7y(y- 2\(x\) - 1)

= 2\(x^3\) + \(x^2\) - 14\(xy\) - 7y - 7y² + 14\(xy\) + 7y

= 2\(x^3\) + \(x^2\) - 7y²

c, (-4\(x^3\)y⁵ + 2\(xy^2\)) : ( - 5\(xy^2\))

= -2\(xy^2\)( 2\(x^2y^3\) - 1) : ( -5\(xy^2\))

= 0,4.(2\(x^2y^3\) - 1)

= 0,8\(x^2y^3\) - 0,4 

-4\(x^n\)y⁵ ⋮ 7\(x^4\).y\(^n\) ⇔ \(\left\{{}\begin{matrix}x.y⋮7\\n>4\\5>n\end{matrix}\right.\) ⇒  S = \(\varnothing\)

Bài 1 :

\(A=-x^2+6x+14\)

\(A=-x^2+6x-9+23\)

\(A=-\left(x^2-6x+9\right)+23\)

\(A=-\left(x-3\right)^2+23\)

Vì \(-\left(x-3\right)^2\le0\)

\(\Rightarrow A=-\left(x-3\right)^2+23\le23\)

\(\Rightarrow Max\left(A\right)=23\)

Bài 2 :

\(B=4x^2+12x+30\)

\(\Rightarrow B=4x^2+12x+9+21\)

\(\Rightarrow B=\left(2x+3\right)^2+21\)

Vì \(\left(2x+3\right)^2\ge0\)

\(\Rightarrow B=\left(2x+3\right)^2+21\ge21\)

\(\Rightarrow Min\left(B\right)=21\)

3\(y\) + \(y\) + (-5\(y\)) = 3\(y\) + \(y\) - 5\(y\) = \(y\).( 3 + 1 - 5) = \(y.\left(4-5\right)\) = -y

3+1+(-5)=-1;

=-1y

=-y

;)))))))

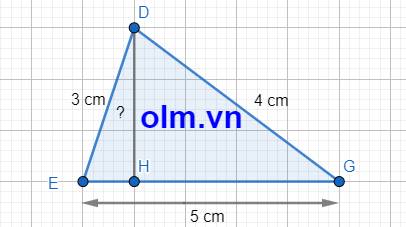
Gọi độ dài cạnh EH là \(x\)  (cm);  0 < \(x< 5\)

Độ dài cạnh HG là: 5 - \(x\) (cm)

Xét tam giác vuông HDE vuông tại H, theo pytago ta có:

DH² = 3² - \(x^2\)  = 9 - \(x^2\)(1)

Xét tam giác vuông DHG vuông tại H theo pytago ta có:

DH² = 4² - (5 - \(x\))²  = -\(x^2\) + 10\(x\) - 9(2)

Từ (1) và (2) ta có: 

-\(x^2\) + 10\(x\) - 9 = 9 - \(x^2\)

         10\(x\) = 18

          \(x\) = 1,8 (thỏa mãn)

Thay \(x\) = 1,8 vào biểu thức (1) ta có:

DH² =  9 - (1,8)² = 5,76

DH = \(\sqrt{5,76}\) = 2,4 (cm)

Kết luận: độ dài đoạn DH là 2,4 cm 

Đây là dạng toán chuyển động cùng chiều, khác thời điểm.

Kiến thức cần nhớ: 

Bước 1: Đưa về chuyển động cùng chiều cùng thời điểm

Bước 2: Tìm thời gian hai xe gặp nhau bằng cách lấy quãng đường chia hiệu vận tốc

Bước 3: Tính thời điểm hai xe gặp nhau bằng cách: lấy thời gian hai xe gặp nhau cộng với thời điểm xe xuất phát lúc sau.

Thời gian xe máy khởi hành trước xe đạp là:

     8 giờ 40 phút - 7 giờ = 1 giờ 40 phút

Đổi 1 giờ 40 phút = \(\dfrac{5}{3}\) giờ

Khi xe máy khởi hành thì xe đạp cách xe máy quãng đường là:

      30 \(\times\) \(\dfrac{5}{3}\) = 50(km)

Thời gian xe máy đuổi kịp xe đạp là:

   50 : (30 - 10) =  2,5 giờ

Đổi 2,5 giờ = 2 giờ 30 phút

    Hai xe gặp nhau lúc :

        8 giờ 40 phút + 2 giờ 30 phút =  11 giờ 10 phút

Kết luận: Hai xe gặp nhau lúc 11 giờ 10 phút

 Điều kiện \(0< x\le120\)

 Số tiền thu được khi bán \(120-x\) món quà là \(x\left(120-x\right)=-x^2+120x\)

 Lợi nhuận thu được là \(-x^2+120x-40x=-x^2+80x\)

 Ta quy về bài toán tìm giá trị lớn nhất của hàm số \(f\left(x\right)=-x^2+80x\). Ta thấy \(f\left(x\right)=-\left(x^2-80x+1600\right)+1600\) \(=-\left(x-40\right)^2+1600\) \(\le1600\). Dấu "=" xảy ra khi và chỉ khi \(x-40=0\Leftrightarrow x=40\) (nhận)

 Như vậy, giá bán một món quà ở đợt này nên là 40 nghìn đồng để lợi nhuận thu được là cao nhất.

Bài yêu cầu gì em?

\(6xy\left(xy-y^2\right)-8x^2\left(x-y^2\right)+5y^2\left(x^2+xy\right)\\ =6x^2y^2-6xy^3-8x^3+8x^2y^2+5x^2y^2+5xy^3\\ =\left(6x^2y^2+8x^2y^2+5x^2y^2\right)+\left(-6xy^3+5xy^3\right)-8x^3\\ =19x^2y^2-xy^3-8x^3\)

Với `x=1/2;y=2` ta có :

 \(19x^2y^2-xy^3-8x^3\\ =19.\left(\dfrac{1}{2}\right)^2.2^2-\dfrac{1}{2}.2^3-8.2^3\\ =19.\dfrac{1}{4}.4-\dfrac{1}{2}.8-8.8\\ =19-4-64\\ =-49\)